Définition de ce cas particulier
Cette situation décrit deux particules restant au contact (ou collées) après la collision.
Seule la conservation de la quantité de mouvement subsiste.
Elle s'écrit :
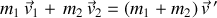
Qu'en est il de la conservation de l'énergie cinétique ?
Le calcul peut être effectué.
Plus précisément, la variation de l'énergie cinétique entre "avant et après le choc" peut être calculée selon :
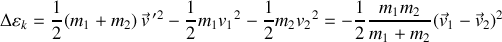
Cette variation d'énergie cinétique est clairement une perte d'énergie puisqu'elle est négative.
Elle s'effectue sous forme de dégagement de chaleur ou de déformation par exemple.
Expérimentalement, elle dépend fortement des surfaces et matériau en contact.
La quantité
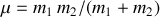, qui apparaît, possède la dimension d'une masse : Une masse réduite des deux corps.
Elle va jouer un rôle non négligeable dans les collisions (particule "relative" ou fictive).
Sa forme rappelle singulièrement l'équivalence entre
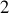résistances électriques en parallèle ou
ressorts en série :
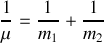
Cette masse est dénommée "réduite" car elle caractérise une masse intermédiaire entre la plus petite et la plus grande.
En cas de déséquilibre important entre les deux,
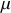prend une valeur proche de la plus petite masse.
La perte d'énergie est également une énergie cinétique proportionnelle à la vitesse "relative" .
D'où l'image d'une perte d'énergie cinétique portée par une particule fictive ("relative") de masse
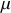et dont la vitesse correspond à la différence des vitesses des deux particules initiales.
La quantité de mouvement totale étant conservée, une description en termes de centre de masse conclut à un CDM en mouvement rectiligne et uniforme.
CDM et particule fictive seront deux des images à conserver de ce chapitre.
Complément : Coefficient de restitution
Les deux situations décrites ci-dessus représentent un cas extrême (complétement élastique) et un cas particulier (complétement mou) entre lesquels se déclinent un panel d'expériences intermédiaires qu'un nouveau paramètre va décrire, toujours associé à l'énergie cinétique.
Le degré d'élasticité d'une collision est mesuré par un coefficient de restitution énergétique,
.
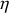Il est mesuré par le rapport entre deux sommes : celle des énergies cinétiques finales sur celle des énergies initiales.
Lorsque ce coefficient est
nul, la collision est parfaitement inélastique ;
égal à l'unité, la collision est parfaitement élastique.
Deux situations extrêmes.
Mais par extension, ce coefficient peut même être supérieur à l'unité : par exemple lors d'un match ou au billard, quand la balle reçoit de l'énergie ponctuellement.
Ces systèmes sont non isolés dans ces phases particulières qui s'intercalent entre les phases d'isolement et doivent être identifiées dans des séquences bien définies.
