i. Le choc élastique 1-D

Ce choc, réalisé sur banc à coussin d'air par exemple, est complétement résolu.

Il est unidirectionnel.

Les vecteurs-vitesses avant et après le choc ont une seule composante : 2 équations pour 2 inconnues.

Dans le cas général, les vitesses après la collision sont données par :

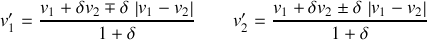
où .

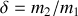Les vitesses sont exprimées en valeur algébrique pour tenir compte de toutes les situations expérimentales possibles : choc frontal, une des particules à l'arrêt, ou les deux se suivant initialement (avec la condition nécessaire... rattraper la première).

Un seul couple de vitesses finales est solution.

La valeur absolue dans les formules et la correspondance des solutions entre les formes 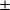et permettent de retenir les réponses que la physique (et le bon sens) accepte.

ii. Le choc élastique 2D

Le choc élastique de deux particules dans le plan horizontal (2-D) est supposé réalisé sur une table à coussin d'air pour éviter les frottements.

Plusieurs cas se déclinent.

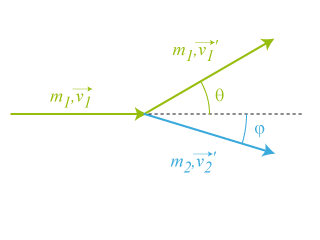
• Si les masses des particules sont égales, pour raison de symétrie, les angles entre leurs directions après la collision et la direction initiale seront égaux. (fig. 15)

• Si de plus l'une est initialement au repos, l'angle entre les deux particules après le choc est de

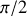
mais nulle information sur le module de chacune des vitesses ne peut être déduite des équations.

Dans le cas général du choc 2-D, il manque toujours une donnée pour résoudre le problème (4 inconnues pour 3 équations).

Néanmoins des informations partielles et angulaires peuvent être obtenues.

Ainsi les relations entre les modules des vitesses et les angles de sortie par rapport à la direction initiale des deux particules (fig. 15), accessibles expérimentalement et données par :

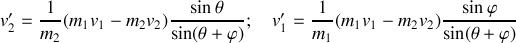
Ces relations sont obtenues à partir de la conservation de la quantité de mouvement.

La conservation de l'énergie conduit à la relation symétrique suivante :

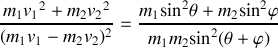
• Lorsque la particule 2 (cible) est immobile (fig. 15), ces équations se simplifient pour donner :

Figure 15 : Collision 2-D avec une particule à l'arrêt

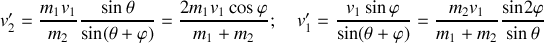
La conservation de l'énergie donne la propriété angulaire suivante :

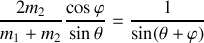
Cette dernière équation permet de retrouver la situation où les deux masses sont égales où .

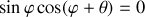Elle décrit les 2 directions possibles des particules après le choc : l'arrêt de celle incidente, le recul de la cible ou leur séparation en équerre.

Quelques résultats complémentaires sont notamment déduits de ce qui précède :

• Après le choc, la valeur 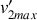est atteinte pour .

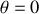• Si la masse 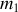de la particule incidente est inconnue, il est possible de la déterminer en réalisant des collisions avec différentes cibles de masse 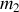connues.

La mesure, dans l'axe de la particule incidente, des maxima des vitesses de recul des particules cible permet d'exprimer le rapport de ces vitesses ( 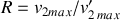) en fonction des masses mises en jeu et de déduire la masse inconnue ( ).

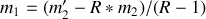Cette expérience de collisions a été utilisée par Chadwick en 1932 pour mesurer la masse du Neutron, les particules cibles étant l'Hydrogène et l'Azote.