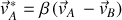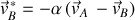Choc et référentiel du CDM
La quantité de mouvement totale étant conservée, avant et après le choc, le déplacement du CDM est rectiligne et uniforme.
Ce point particulier est donc porteur d'un référentiel galiléen.
Le mouvement des 2 corps peut être décrit dans le référentiel galiléen du CDM,
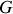. (fig. 16)
Les particules sont notées
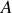et
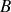, de masses respectives
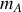et
.
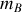Toutes les grandeurs repérées dans le référentiel du CDM seront marquées d'une étoile
.
Ainsi
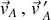et
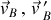sont les vitesses dans le référentiel du laboratoire, 
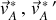et
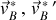sont les équivalents dans celui du CDM.
Les relations de passage entre les grandeurs sont données par :
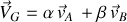
Les notations suivantes ont été adoptées :
Avant le choc.
Les écritures suivantes :
et
seront utiles pour la suite des calculs.
Ainsi que cette propriété remarquable du CDM :
.
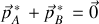Remarque : Énergie cinétique totale
Le calcul des énergies cinétiques dans le référentiel du CDM et celui du laboratoire permet de vérifier le bilan en énergie cinétique.
Et ... de ne pas oublier le déplacement du CDM.
Dans le référentiel du CDM :
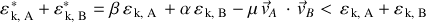
La somme des énergies cinétiques dans le référentiel du laboratoire inclut également celle du CDM (représenté par une particule de masse
).
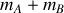L'énergie cinétique du CDM s'écrit :
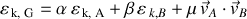
Elle dépend de la masse réduite
.
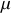La propriété
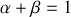est alors utilisée pour vérifier l'égalité :
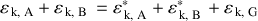
Les énergies, dont cinétiques, sont additives.
Après le choc :
La quantité de mouvement totale dans le référentiel du CDM reste inchangée avant et après le choc.
Cette propriété s'écrit :
.
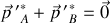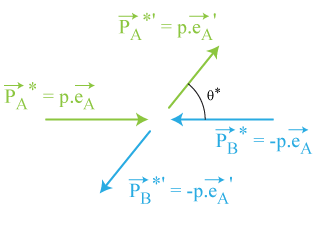
Les particules finales ont donc toujours des impulsions égales et opposées.
De plus, l'énergie cinétique du CDM (sa vitesse est constante) est invariante avant et après le choc.
L'énergie cinétique totale étant conservée, la relation suivante entre les énergies cinétiques des particules peut être déduite :
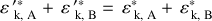
Exprimée en fonction des impulsions, cette dernière relation conduit à une égalité en module des impulsions avant et après le choc soit :
.
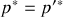Dans le référentiel du CDM, la direction de
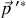n'est pas déterminée ; seul son module l'est.
Ainsi
1) toutes les directions, modulo
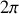et centrées sur
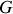, sont équiprobables et 2) les impulsions après le choc dans le référentiel du CDM se trouvent sur un cercle de rayon
.
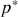Restent alors à déterminer les directions les plus probables de sortie du choc, avec notamment un cône de "sortie" des particules.
Deux voies permettent de s'approcher de la solution :
une voie graphique, toujours imparfaite mais qui permet de visualiser les réponses. (fig. 17)
Elle est présentée ci-après.
une méthode, plus générale et globale, basée sur la théorie de la diffusion.
Méthode : Résolution graphique
Une direction arbitraire
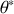est choisie pour l'angle de sortie.
Le retour vers le référentiel du laboratoire est obtenu en recomposant les vitesses au moyen du déplacement du CDM comme effectué sur la fig. 17.
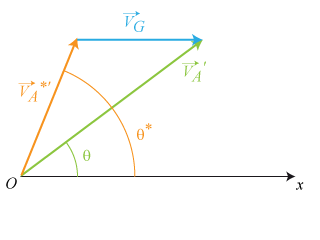
Un traitement géométrique de la fig. 17 permet de déduire les relations d'angle suivantes :
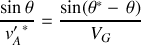
L'angle maximum de diffusion peut être déduit par dérivation :
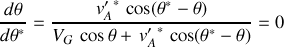
La solution générale s'écrit :
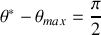et
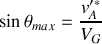
Cet angle maximum est l'angle du cône dans lequel les particules vont diffuser selon une distribution spatiale que cette résolution ne permet pas de déduire.
Complément : Les masses sont égales
Tout ce qui précède peut être appliqué au cas particulier de masses égales.
Elle permet une visualisation graphique des symétries d'une telle situation dans le référentiel du CDM.
La propriété
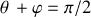constitue un bon repère d'analyse.
Dans le cas d'une cible à l'arrêt, le référentiel du CDM n'apporte rien de plus par rapport à l'analyse ci dessus... le mouvement de la cible dans ce référentiel est également présent.
Une autre approche permet d'aborder le choc ou la collision d'un flux de particules sur des cibles avec l'approche spécifique de la section efficace de diffusion.
Cette méthode est valable aussi bien pour les chocs que pour les collisions.
Elle nécessite la notion de paramètre d'impact commun aux deux problèmes.
De ce fait et avant d'aborder la théorie de la diffusion, le traitement différencié de la zone d'impact d'une collision constitue un complément utile.
Ce qui suit présente également une démarche nuancée pour approcher et cerner un peu plus la zone d'impact quand la loi d'interaction est connue.
