Introduction
A titre de rappel :
Un solide indéformable possède 6 degrés de liberté.
Trois coordonnées sont nécessaires pour décrire le mouvement global du solide dans un référentiel fixe
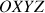, celui du centre d'inertie dans le formalisme vectoriel (théorèmes généraux).Trois variables angulaires pour décrire l'orientation du solide par rapport à des directions initiales, toujours notées
,
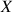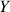et
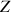mais centrées sur un point préalablement défini du solide.
Plusieurs conventions existent pour définir ces
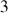rotations.
Celle retenue dans ce cours est celles des angles d'Euler, caractérisant les trois rotations les plus générales que peut effectuer un solide à partir de ses directions initiales
,
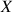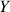et
.
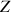Ces rotations sont associées à tout type de solide et s'effectuent dans un référentiel dont le centre est un point de celui-ci, noté
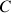, qui peut être préférentiellement confondu avec le centre de masse ou d'inertie
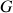. (Fig. 14)
Même si des variantes existent, selon les sens, axes de rotation choisis et l'utilisation qui en est faite, les angles d'Euler sont associés au théorème d'Euler (1776) dont l'énoncé est :
Quomodocunque sphaera circa centrum suum conuertatur, semper assignari potest diameter, cuius directio in situ translato conueniat cum situ initiali.
Quand une sphère tourne autour de son centre, il est toujours possible de trouver un diamètre dont la position finale correspond à celle initiale.
Ce théorème trouve une démonstration aisée avec le choix des
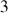rotations d'Euler qui seront développées dans ce cours.
Toute rotation d'un solide dans l'espace, représentée par un vecteur vitesse angulaire
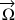, sera ainsi composée à partir de ces rotations d'Euler : elles constituent donc une base angulaire pour composer toute rotation dans l'espace.
Concrètement et partant d'un repère d'espace fixé au solide, toute position ultérieure peut être déduite d'une succession de trois rotations énoncées à partir de celles d'Euler.
Ces trois angles permettent le passage d'une position initiale du solide, caractérisée par le référentiel fixe (
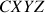), à une position finale issue de
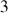rotations et représentée par le référentiel mobile (
).
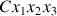Ces deux référentiels, avant et après les rotations, ont généralement tous deux pour axes, les axes principaux d'inertie du solide, conformément aux règles décrites précédemment.
Ainsi dans le cas général, la rotation finale du solide est une somme algébrique de ces
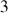rotations.
En termes de vecteurs vitesses angulaires (portés par les axes de rotation), le vecteur final
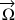est la somme des
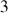vecteurs vitesses angulaires qui seront définis. Ainsi l'axe de la rotation finale a sa propre direction, en général distincte de celles des axes principaux (propres) du solide (mobiles car fixés aux solide).
Ce chapitre comporte
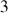parties.
Après la définition de la base d'Euler, des applications de ces rotations seront proposées, tournant essentiellement autour de mouvements de toupies symétriques... Ainsi en plus de leur précession, le phénomène de nutation sera présentée.
Dans la dernière partie, les équations d'Euler permettent de revenir à une description du mouvement dans le référentiel
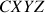. Cette étape est nécessaire avant la prise en compte du mouvement global éventuel.
