Les variables de base décrivant le mouvement d'un système mécanique sont souvent associées aux coordonnées
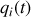des points composant le système.
Le formalisme lagrangien, lui, est construit à partir des coordonnées mais également des vitesses notées :
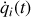, représentant la dérivée temporelle des coordonnées.
La variable, dans le formalisme lagrangien, peut donc représenter soit la coordonnée soit la vitesse.
Deux notions importantes sont nécessaires pour définir la variable généralisée : la contrainte sur les variables et le degré de liberté.
Dans toute cette partie,
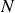particules sont considérées, notées
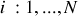, nécessitant
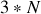coordonnées dans l'espace à trois dimensions.
Le temps n'est pas une variable comme les autres en mécanique classique : il jouera un rôle particulier, celui de paramètre continu.
Les contraintes seront distinguées selon deux types.
Les définitions sont ici données en toute généralité.
Définition : La contrainte holonome
La contrainte holonome est une relation liant les variables du problème et le temps.
C’est une fonction
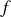différentiable en tout point qui vérifie la propriété suivante :
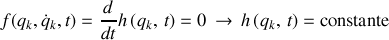
L'existence de la fonction
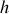, une "surface multidimensionnelle", garantit la différentiabilité de
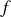, mais également l'existence d'une forme de constante du mouvement.
En pratique, cette contrainte traduit le fait qu’une coordonnée peut s’exprimer en fonction des autres ce qui réduit d'une unité le nombre de variables réellement inconnues et utiles à la description du système.
La contrainte holonome peut être de plus soit :
Scléronome si
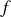ne dépend pas explicitement du temps.Elle décrit alors un système physique fermé, sans échange d'énergie avec le milieu extérieur.
Les forces qui s'y appliquent répondent au principe d'action et de réaction.
C'est le cas du système conservatif.
Rhéonome si
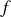dépend explicitement du temps. Le système décrit est ouvert et permet les échanges d'énergie.
C'est le cas, par exemple, d'une tige horizontale ou d'un cerceau vertical tournant autour d'un axe de symétrie, vertical, avec une vitesse angulaire constante ou non : un couple moteur apporte de l'énergie au système.
L’intérêt de ce type de contraintes réside dans la détermination des solutions : les problèmes dits holonomes ont formellement toujours une solution.
À l'opposé, il n’existe pas de méthode générale pour résoudre un problème non holonome, tel celui dépendant de puissances de la vitesse par exemple.
De même, les contraintes sous forme d'inégalités constituent des contraintes non holonomes.
Définition : De la contrainte à la notion de degré de liberté
Si le système de
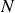particules est soumis à
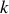contraintes, le nombre de degrés de liberté, noté
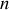, est :
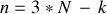
Et le formalisme lagrangien est décrit par
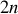variables généralisées : coordonnées et vitesses.
Exemple : Quelques exemples familiers
1) Pour décrire un pendule simple (dans l'approximation du point matériel) en mouvement plan, 2 contraintes s'exercent :
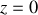et
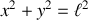, si le mouvement a lieu dans le plan
.
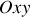Ainsi
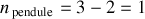. La coordonnée généralisée est alors une variable angulaire.
Lorsque le mouvement du pendule est conique, le pendule a
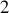degrés de liberté puisque
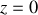n'est plus une contrainte valide.
Lorsque le pendule a un mouvement plan mais est élastique, le nombre de degrés de liberté est également
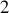car la contrainte associée à la longueur du pendule n'existe plus.
2) Le solide indéformable (corps rigide) est caractérisé par un nombre
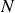(très grand) de particules dont la distance entre 2 particules quelconques est constante.
Le décompte de ces contraintes, dans le cas d'un mouvement général dans l'espace, conduit à un nombre de degrés de liberté
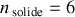répartis comme suit :
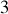variables décrivent le mouvement global du solide dans l'espace (la translation du CDM, par exemple) et
-
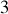autres, des rotations spécifiques du solide autour de
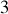axes qui lui sont associés et exprimées dans un référentiel fixé au solide.
De fait,
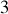points quelconques dans l'espace sont suffisants pour décrire le mouvement d'une structure solide : la position de tous les autres points peut être déduite, les distances
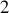à
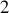étant fixes.
Les distances, fixes, entre les
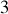points sont des contraintes,
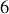variables seulement suffisent pour suivre son évolution dans l'espace et au cours du temps.
3) Dans le cas d'un disque vertical roulant sans glisser sur un plan horizontal, le long d'un axe
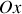par exemple :
.
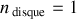Le mouvement du CDM est linéaire (nécessitant une variable).
Le solide n'a qu'une rotation, autour de l'axe perpendiculaire au plan du disque, nécessitant une seconde variable, angulaire.
Ces deux variables sont reliées par la contrainte du roulement sans glissement (
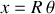, où
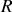est le rayon du disque).
Si le glissement a lieu,
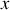reprend sa 'liberté' et devient une variable indépendante de
.
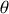Si le mouvement a lieu dans le plan horizontal
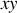, avec le disque toujours vertical, un degré de liberté de plus est regagné par le CDM et un autre par une rotation possible autour d'un axe vertical contenu dans le plan du disque.
La condition de roulement sans glissement associera la longueur parcourue dans le plan et la rotation autour de l'axe parallèle au plan.
Un cas particulier de solide :
Pour une tige rigide, le nombre de degrés de liberté est
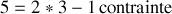. Comparativement au solide, une rotation disparaît : celle selon l'axe de la tige (filiforme).Il en est de même pour une molécule diatomique linéaire.
Mais alors que la tige est rigide, la molécule possède un mouvement supplémentaire dans l'espace à 3 dimensions : elle vibre autour d'une position moyenne le long de l'axe des atomes. Mais ce dernier mouvement peut être isolé pour ne conserver que les 5 degrés de liberté de la tige (ce qui revient à effectuer un zoom sur le mouvement spatial, l'isoler).
L'objectif de ce qui suit est d'exprimer les lois de la mécanique en fonction des coordonnées généralisées, indépendantes et correspondant aux
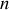degrés de liberté :
.
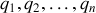Explication : Variables indépendantes à priori.
Dans le formalisme lagrangien qui suit,
variables généralisées sont considérées, toutes considérées comme indépendantes les unes des autres : les coordonnées mais également leurs vitesses généralisées associées.
La propriété d'indépendance des coordonnées généralisées entre elles est validée par la notion de degré de liberté.
L'application des conditions s'appliquant au mouvement (lois de la mécanique) produit des équations du mouvement dont la résolution se traduit par une trajectoire liant les coordonnées.
Mais la propriété d'indépendance des coordonnées avec leurs vitesses associées paraît présupposée.
C'est une condition assumée par le principe variationnel.
De même, ce qui peut lier ces
variables indépendantes au départ, ce sont les interactions qu'intègrent les fonctionnelles décrivant le système et qui s'expriment ultérieurement par les équations du mouvement déduites du formalisme.
En mécanique vectorielle, les lois régissant le mouvement mettent en jeu les dérivées temporelles de l'impulsion (ou quantité de mouvement) et du moment angulaire (ou moment de la quantité de mouvement) : ce sont ces grandeurs, définies à partir des vitesses, qui varient sous l'action des interactions, entraînant par intégration l'existence des trajectoires.
Les mettre en jeu au même titre que les coordonnées dans un formalisme semble cohérent.
Remarque : Schéma global
En mécanique, le problème est vu en trois phases.
La première est celle de la reconnaissance du système et de ses limites, l'identification des contacts aux limites, de ses contraintes : mouvement plan, sphérique..., et finalement la déduction de ses variables : coordonnées et vitesses indépendantes.
La seconde analyse plus en profondeur l'origine des observations ou mesures, l'influence des interventions extérieures (interactions longue portée, frottements et autres apports extérieurs). C'est la fonctionnelle qui lie l'ensemble des variables.
L'application du principe de moindre action à la fonctionnelle donne alors les équations différentielles du mouvement qui, intégrées, relient toutes les variables précédemment indépendantes dans des trajectoires.
Attention :
Cette dernière remarque pointe l'importance des phases d'analyse, synonyme de modèle et de conditions d'application.
Elle contribue à la déduction du nombre exact de degrés de liberté... même si une alternative à la réduction du nombre de variables existe.
