Plusieurs évaluations de la fonctionnelle action
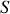permettent d'en déterminer celle qui l'optimise. Pour cela, plusieurs trajectoires,
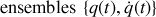, doivent être sollicitées.
Une propriété de l'optimum est que, à son voisinage et entre deux trajectoires proches, la variation de valeur de l'action doit être négligeable ou nulle. Une propriété qui généralise à plusieurs variables l'annulation de la dérivée.
Deux trajectoires proches serviront donc à évaluer l'action.
La condition d'optimisation de l'action s'écrira :
.
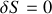Démonstration :
Pour déterminer LA trajectoire qui minimise l'action, la procédure consiste donc à considérer plusieurs trajectoires et à leur appliquer la contrainte d'optimisation.
L'hypothèse majeure du principe de moindre action est la détermination parfaite des points extrêmes, en termes de grandeurs généralisées.
Quelle que soit la trajectoire considérée, sa position aux instants
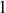et
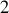est exactement déterminée.Ces points de coïncidence de toutes les trajectoires seront notés
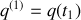et
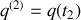.Ils sont caractérisées par des variations d'une trajectoire à l'autre identiquement nulles :
.
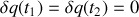La variation, notée
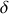, représente le passage d'une trajectoire à l'autre.
Ainsi dans l'intervalle de temps implicite
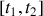deux trajectoires sont choisies, très proches l'une de l'autre.
Elles sont notées
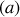et
.
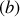La trajectoire de référence, celle recherchée
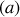, est caractérisée par les coordonnées généralisées
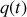et la seconde par
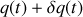permettant ainsi quelques variations de trajectoires.Il en est de même pour les vitesses.
Dans ce qui suit, le symbole
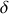représente bien le passage d'une trajectoire à l'autre alors que celui
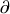représente une variation de la fonctionnelle autour d'une de ses directions de déploiement, mais sur la même trajectoire.
Chaque trajectoire est décrite par son lagrangien et sa propre action (fonctionnelle) de sorte que le principe de moindre action peut s'écrire :
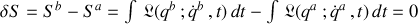
ou encore :
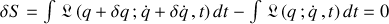
Les trajectoires, idéalement très proches, entraînent de petites variations autorisant des développements perturbatifs dans
.
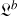Ainsi :
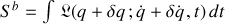
admet le développement suivant :
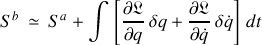
l'intégrale s'effectuant entre les instants
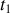et
.
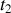En vertu de la distributivité de la dérivée par rapport à la soustraction, dérivée temporelle et variation de trajectoire sont commutatives selon :
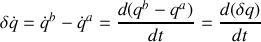
Cette opération, effectuée, met en évidence une dérivée temporelle qui peut être associée à une des deux contributions de la dérivée d'un produit de fonctions :
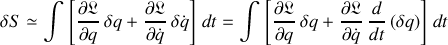
Ce terme de dérivée totale par rapport au temps donne alors lieu à la soustraction des deux termes, isolés dans l'expression suivante :
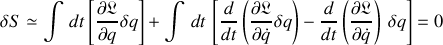
Le terme central est intégrable entre
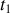et
.
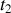Sa contribution est nulle puisque les positions
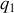et
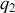sont définies identiques aux trajectoires : la variation produite par un changement de trajectoire est nulle.
Les deux termes qui restent sont regroupés et produisent la relation intégrale suivante :
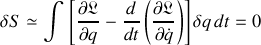
L'intégrande est nul puisqu'il compare des évolutions entre des trajectoires très proches et ce pendant la durée
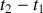. Outre qu'elles sont continues, leur proximité fait que le passage de l'une à l'autre ne devrait pas entraîner de changement de signe.
L'équation du mouvement d'Euler-Lagrange, d'un système décrit par le lagrangien
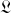est déduite :
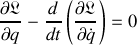
Elle définit l'équation différentielle de la trajectoire qui minimise l'action.
Fondamental : Généralisation à n dimensions
Utilisant la même méthode que ci-dessus, la généralisation à
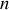degrés de liberté, indépendant les uns des autres, produit la variation d'action suivante :
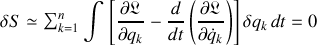
L'intégrale porte sur le temps.
Les variations de coordonnées généralisées s'effectuent pour
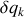, d'une trajectoire à l'autre et 
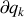, sur la même trajectoire.
L'indépendance de ces variables entraîne une contribution nulle de chaque terme de la sommation. Chaque intégrale individuelle est nulle.
Il en est de même pour chaque intégrande.
Définition :
Pour un système comportant
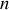degrés de liberté, décrit par la fonction de Lagrange suivante :
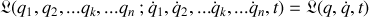
le principe variationnel ou principe de moindre action permet de dériver les équations d'évolution suivantes :
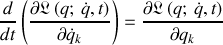
où
.
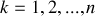Ces
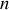équations différentielles du second ordre pour les
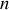degrés de liberté décrivent complétement le mouvement du système.
Ce dernier étant encore indéfini, son lagrangien l'est également.
Remarque : Un cas particulier.
Pour un système conservatif et lorsque les coordonnées généralisées sont identiques aux coordonnées spatiales du système de points matériels, dans un référentiel cartésien par exemple, l'énergie cinétique seule dépend des vitesses alors que l'énergie potentielle dépend uniquement des coordonnées.
Si le lagrangien est donné par la différence de ces deux énergies, alors :
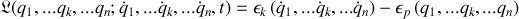
Les dérivées partielles par rapport aux vitesses mettent en jeu l'énergie cinétique et contribuent aux termes d'inertie.
Celles par rapport aux positions concernent l'énergie potentielle et contribuent aux forces mises en jeu.
Cette séparation entre les types de variables généralisées et les énergies de la fonction de Lagrange permet de reconnaître, dans le système d'équations d'Euler-Lagrange, les équations du mouvement de Newton dérivées de son second postulat.
