Tout système mécanique est caractérisé et décrit par une fonctionnelle du temps, des coordonnées généralisées ET des vitesses associées.
Elle est notée :
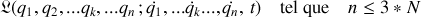
Pour simplifier la notation, l'ensemble des coordonnées généralisées
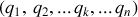est notée
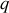, et celui des vitesses généralisées
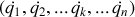notée
.
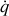Ces variables généralisées ont leur espace de représentation permettant de "visualiser" les états et donc l'évolution du système mécanique.
Cet espace sera présenté après l'énoncé du principe qui suit.
Fondamental : Énoncé du principe de moindre action.
Si aux instants
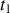et
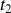, le système occupe respectivement deux positions
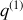et
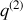, exactement définies, alors entre ces deux instants son évolution est telle que son intégrale d’action ou fonctionnelle action
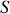notée :
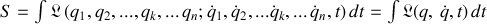
est extrémale.
La fonctionnelle
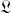est la fonction de Lagrange ou lagrangien.
Remarque : Une interprétation du principe.
Ce principe exprime une forme d'unicité de la fonctionnelle lagrangienne pour un système parfaitement identifié en termes de toutes ses variables généralisées entre deux instants
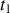et
.
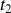Ou encore si le lagrangien décrit bien le système, alors son évolution optimise son intégrale d'action.
Cette formulation mécanique du principe de moindre action, ainsi associée à la description de l'évolution du système au cours du temps, interpelle sur le rôle particulier joué par cette dernière "variable".
Explication : Une formulation variationnelle.
Autrement formulé, le principe de moindre action ou principe de Lagrange-Hamilton postule l’existence d'UNE TRAJECTOIRE (une évolution) parmi d'autres qui réalise
.
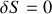Cette trajectoire particulière apportera quelques indications sur la fonctionnelle dénommée lagrangien et permettra de déduire quelques unes de ses propriétés.
Les variables généralisées étant les coordonnées et les vitesses, leurs évolutions au cours du temps peut donner lieu à une représentation graphique dans cet espace particulier.
Définition : Une curiosité pratique : l'espace des phases ou espace de configuration
L'espace des phases ou de configuration a donc
dimensions.
Ses
axes correspondent aux coordonnées
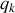et vitesses
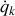généralisées, où
.
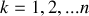Les trajectoires ou surfaces multidimensionnelles représentent les fonctionnelles (fonctions de fonctions) décrivant le système.
La fonction de Lagrange
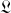, moyennant certaines conditions, peut y être représentée.
Syntaxe : Et le temps ?
Dans cet espace, le temps
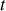n'apparaît pas. Il est implicite.
Régissant les variables généralisées,
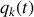et
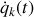, le passage d'une position à l'autre ne peut se faire sans son écoulement.
Même l'immobilité caractérisant une réponse stationnaire n'empêche pas cet écoulement.
Cette espace de configuration permet donc de visualiser des formes de trajectoires.
Surtout celles, particulières, vérifiant les lois de conservation susceptibles d'être établies et mettant en jeu les grandeurs généralisées correspondantes.
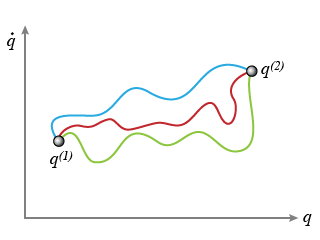
Exemple : Espace de configuration bidimensionnel
À deux dimensions, une trajectoire entre deux instants
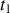et
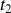est représentée sur la figure ci après, (Fig. 8), où sont notées les positions extrêmes 1 et 2.
Entre les deux points représentés, une infinité de trajectoires peuvent se déployer selon le système étudié, la fonctionnelle susceptible de le décrire et ses propriétés.
Plus généralement et pour un système décrit par
variables généralisées (coordonnées et vitesses), un tel diagramme
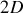constituera une projection sur le plan réduit
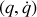de la représentation multidimensionnelle.
Dans le complément et exemple qui suit, la représentation de la fonctionnelle "lagrangien" selon l'espace des configurations n'apporte qu'une visibilité différente au problème.
Mais la conservation de la fonctionnelle "énergie totale" permet de visualiser les trajectoires, donc les solutions.
Complément : Exemple d'espace des phases
Dans l'étude d'un pendule simple en mouvement plan (Fig. 2), de masse
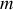et de longueur
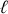(par exemple, une tige rigide de masse négligeable et à l'extrémité de laquelle est accrochée la masse
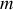) le lagrangien, défini dans le chapitre précédent comme une différence entre énergies cinétique et potentielle, s'écrit en coordonnées polaires :
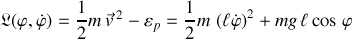
Moyennant quelques changements de paramètres, le lagrangien prend une forme plus simple.
Ainsi
une énergie de référence, constante,
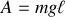, et un paramètre continu sans dimension :
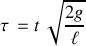, représentant une nouvelle phase
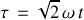, pondérée par un multiple non entier de la pulsation propre de toute trajectoire périodique. Mais cela représente également une mesure du temps rapportée à une fraction de la période
: 
.
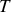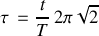le passage à de nouvelles variables généralisées
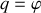et
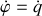en
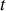mais pas en
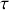selon
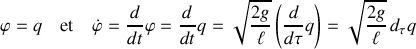
transforment le lagrangien du pendule :
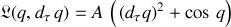
La dérivée temporelle est donc rapportée à la nouvelle échelle de temps
.
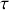Cette forme met en évidence l'énergie potentielle de référence
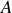: une constante porteuse d'une nouvelle mesure du temps et... qui suggère une normalisation du lagrangien.
L'espace de configuration comporte 2 dimensions.
Les valeurs de la fonctionnelle
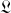, ajoutée à cet espace, fournit un troisième axe permettant de décrire une surface dans un espace à
dimensions.
Ainsi si une valeur particulière
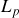de la fonctionnelle
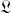existe, elle permettra de définir le paramètre sans dimension
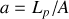et de découper dans le plan
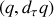une trajectoire curviligne décrivant la condition particulière du système dans l'espace des phases.
Pour de faibles valeurs des variables
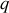, un développement en série du cosinus permet de dériver
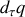en fonction de
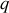, paramétré par
.
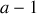Mais ce n'est pas le lagrangien qui permet une visualisation des trajectoires dans l'espace des phases.
Pour cela, une grandeur conservée, ou constante du mouvement, est plus adaptée. Voir plus loin.
Par ailleurs, les changements de variables et de formes du lagrangien ne modifient en rien l'évolution du pendule.
Les équations du mouvement du pendule dans les deux notations (et espaces de configuration) sont similaires :
.
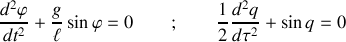Le facteur
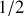vient du choix de "l'échelle caractéristique de temps", plus rapide de
.
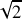Pour de faibles inclinaisons, ce système décrit des oscillations harmoniques.
Mais pour des angles plus élevés, une approche perturbative non linéaire permet un développement analytique des équations du mouvement et la détermination de solutions approchées.
Un choix de variables légèrement différent sera effectué avec l'analyse de l'énergie mécanique, grandeur conservée pendant le mouvement.
La forme analytique des solutions n'étant pas accessible pour de grandes amplitudes angulaires, une représentation graphique permet de déterminer l'allure des trajectoires dans l'espace des phases.
Explication : Système conservatif et énergie mécanique
L'énergie mécanique totale permet donc une résolution géométrique et visuelle.
La conservation de la fonctionnelle "énergie mécanique totale" met en évidence les trajectoires dans l'espace des phases (
,
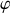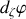) où
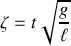est l'échelle de temps rapportée à la pulsation propre.
L'énergie mécanique s'écrit, avec le temps réel :
.
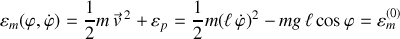Les notations choisies ici, comme
une échelle de temps
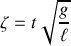et une énergie mécanique initiale la plus générale possible
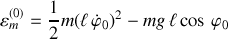
(énergie cinétique et inclinaison initiales)
permettent d'écrire la conservation de l'énergie mécanique sous une forme épurée, soit :
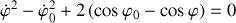
où la dérivation temporelle (point) est effectuée par rapport à
.
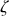Une première étude graphique de cette équation permet de visualiser les trajectoires possibles pour différentes conditions initiales.
L'analyse pour déduire l'allure des trajectoires peut être progressive et menée d'abord avec la condition
.
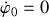L'effet d'une énergie cinétique initiale non nulle consistera globalement à
déplacer le faisceau de trajectoires sur l'axe des vitesses angulaires pour certaines phases initiales (faibles angles), et à
élargir (selon l'axe des phases) les trajectoires.
Pour des angles initiaux plus grands, une énergie cinétique initiale suffisante peut induire un basculement de l'autre coté d'une séparatrice, apparaissant dans l'analyse qui suit.
Une séparatrice entre états périodiques, confinés et non confinés.
Explication : Des équations, des formes de trajectoires.
La description des trajectoires dans l'espace des phases
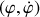est basée sur
la propriété suivante :
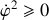, assurant une racine carrée réelle, et quelques points particuliers : ceux d'intersection avec les axes.
L'équation maîtresse des trajectoires exactes est directement déduite de la fonctionnelle "énergie mécanique totale".
Elle est donnée par :
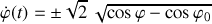
issue de la forme plus générale, avec vitesses initiales :
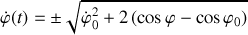
Cette forme complète permet de suivre pas à pas le complément apporté par l'existence d'une vitesse initiale.
Les principales propriétés des trajectoires sont les suivantes :
Elles sont paramétrées par
.
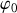Pour un angle initial positif, la racine carrée est réelle lorsque
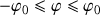.Ceci est un signe de trajectoire symétrique, périodique et fermée.
Lorsque
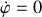est réalisée, donc pour des vitesses angulaires nulles, la trajectoire coupe l'axe des angles.Les points d'intersection sur l'axe angulaire sont :
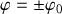.- Ces valeurs seront plus élevées en cas de vitesse initiale non nulle : les oscillations du pendule auront de plus larges amplitudes.
Lorsque
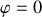, l'intersection avec l'axe des vitesses angulaires correspond aux valeurs maximale et minimale atteintes par la vitesse angulaires.Ces deux valeurs sont symétriques et valent :
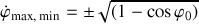. - Ces valeurs sont également plus élevées en cas de vitesse initiale.
Au voisinage de ces deux points particuliers, les pentes sont accessibles par l'utilisation de dérivées et un calcul perturbatif... comme pour toute étude graphique.
Ainsi la pente des trajectoires est formellement donnée par :
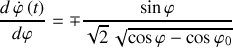
Elle doit être évaluée au point étudié.
Ainsi au voisinage du point d'intersection avec l'axe angulaire,
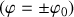, un développement limité de
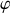est nécessaire.
Il produit à l'ordre dominant :
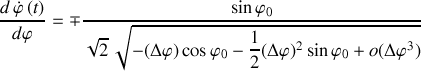
L'expression ci dessus n'est valide que si
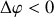impliquant
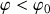ou
ce qui est conforme à la solution de trajectoire confinée, fermée.
Elle permet également de déduire 2 propriétés relatives à l'allure des trajectoires :
Lorsque
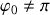, la pente de la tangente au voisinage du point d'intersection est proportionnelle à
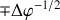.Elle est donc nulle en ce point ce qui implique une tangente verticale et une trajectoire arrondie vers l'origine des phases (courbure).
Lorsque
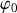se rapproche de
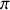, la pente de la tangente est proportionnelle à
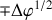impliquant une tangente plus inclinée sur l'axe des angles et une trajectoire plus pointue sur l'axe des phases.
En résumé, pour des angles initiaux tels que
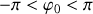, l'angle
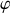du pendule décrit un mouvement compris entre
.
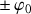Il est harmonique pour de faibles angles : un développement limité des cosinus permet d'obtenir des trajectoires circulaires dans l'espace des phases.
La trajectoire devient de plus en plus anharmonique (moins circulaire : aplati au voisinage de
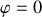(axe des vitesses angulaires) et pointu sur l'axe
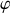au voisinage de
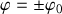) au fur et à mesure de l'augmentation de l'angle initial.
Les trajectoires sont toujours fermées. (Fig. 9)
La situation initiale :
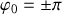décrit une séparatrice (sans vitesse initiale).
La trajectoire peut être fermée avec un retour en arrière de la masse ou au contraire ouverte avec un passage vers la trajectoire voisine
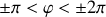mais de façon aléatoire en cas d'opération sans vitesse initiale.
- Une vitesse initiale supprime le coté aléatoire puisqu'elle imprime un sens et une quantité d'énergie supplémentaire disponible.
Les points
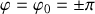deviennent des points d'inflexion. (Fig. 9)
Cette description des trajectoires se reproduit
.
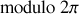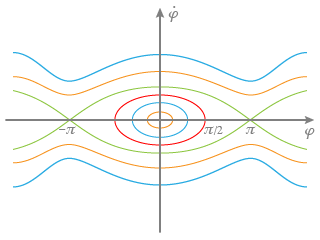
Pour décrire les trajectoires ouvertes, la présence de la vitesse angulaire initiale devient nécessaire.
Cette énergie supplémentaire initiale permet à la coordonnée angulaire de dépasser la limite de la séparatrice et de l'angle limite
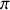pour augmenter indéfiniment en valeur absolue en l'absence de frottements.
Ces trajectoires ouvertes caractérisent notamment la tige qui possède suffisamment d'énergie initiale pour tourner toujours dans le même sens. (Fig.9)
Le niveau d'énergie cinétique initiale doit dépasser un seuil pour que le mouvement soit harmonique.
Pour le formalisme lagrangien, la trajectoire dans l'espace de configuration présente un intérêt car, si le mouvement a lieu, à tout instant le système peut être repéré par une coordonnée et une vitesse généralisée.
Cette représentation permet d'imaginer des trajectoires dont une doit satisfaire au principe de moindre action.
Rappel :
Pour démontrer le principe de Lagrange-Hamilton, sera privilégiée la formulation relative à l'existence d'UNE TRAJECTOIRE particulière qui réalise une action optimum, donc mathématiquement
.
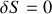Cette trajectoire est décrite de manière unique par une fonction particulière appelée lagrangien, et caractérisant le système physique.
