Avant de traduire le formalisme de la mécanique vers l'optique, quelques rappels d'optique géométrique sont nécessaires.
Rappel : Un peu d'optique géométrique
Le principe de Fermat est un principe variationnel qui s'énonce comme suit :
Entre deux points de l'espace, le rayon lumineux suit la trajectoire de moindre durée
Ce principe minimise le temps de parcours entre les deux points : cette durée peut faire office de fonctionnelle "action".
Si un lagrangien est élaboré, des équations de type Euler Lagrange peuvent être dérivées.
Méthode : Quel lagrangien et quelles équations ?
Pour les notations :
L'indice de réfraction du milieu est noté
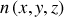et
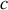la célérité de la lumière.La vitesse du rayon lumineux dans le milieu est
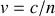de sorte que la distance parcourue pendant un intervalle de temps
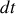est
.
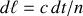La durée du trajet entre les deux points s'écrit alors :
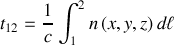
L'élément de déplacement doit être exprimé, en coordonnées cartésiennes par exemple :
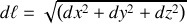
Pour aller plus loin, les conditions expérimentales peuvent être précisées.
Souvent, en optique et en fonction de la géométrie des éléments optiques placés sur le parcours du faisceau lumineux, un plan
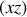suffit pour décrire un rayon lumineux.
Ce plan contient la direction de propagation
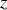et axe de symétrie du système optique (l'axe optique).
La direction
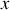exprime l'inclinaison du faisceau par rapport à sa direction de propagation. Cette inclinaison permet de mesurer l'écart aux conditions de stigmatisme de Gauss.
Cette approximation revient à supposer une équivalence structurelle entre les directions
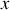et
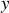, plus simplement à considérer un fin faisceau cylindrique permettant de négliger la forme spatiale transverse du rayon lumineux, et ainsi à supposer une symétrie de révolution autour de l'axe optique.
La variation d'indice va s'effectuer dans ce plan,
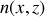, voire même uniquement le long de l'axe
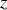pour exprimer les relations de propagation en optique géométrique.
Dans cette description, l'élément de déplacement s'écrit :
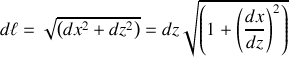
où la propagation est mise en exergue, simulant ainsi le temps qui s'écoule.
L'action à minimiser s'écrit alors :
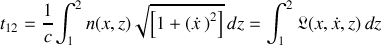
Pour minimiser l'intégrale d'action et déduire les équations du "mouvement", ici de propagation, il faut définir les équivalents des "coordonnées" et "vitesses" généralisées de ce système : l'adjectif 'généralisé' prend alors plus de sens.
Par similarité de notations,
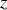paraît assimilable au temps.
Et
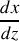peut être notée
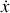: les valeurs de cette dérivée paramètre le stigmatisme.
Cette symétrie de propagation est un problème à un degré de liberté.
L'identification terme à terme, entre la formulation mécanique de l'action et celle du principe de Fermat de l'optique géométrique, produit le lagrangien suivant :
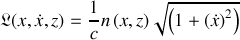
En résumé :
Le paramètre continu
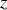, remplaçant le temps
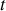, représente l'axe de symétrie du système et la direction de propagation, sous entendant une distance parcourue au cours du temps.La coordonnée généralisée
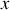est la coordonnée spatiale, normale à l'axe de propagation.Et la vitesse généralisée
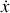mesure l'inclinaison du rayon par rapport à la direction de propagation.
Le rapport
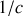, constante réelle, n'a aucune influence en vertu des propriétés du lagrangien.
Il est conservé pour le sens physique qu'il apporte.
L'équation d'Euler-Lagrange devient :
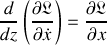
Les dépendances en la coordonnée généralisée,
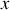, et en
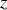sont toutes deux contenues dans l'indice de réfraction dont l'influence est primordiale.
Le calcul des différents éléments de l'équation d'Euler-Lagrange est direct.
Ainsi :
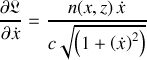
À présent, plusieurs cas de figures peuvent être explorés.
Exemple : Cas d'une réfraction
1) L'indice ne dépend pas de
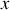ou encore l'indice de réfraction varie selon l'axe de propagation
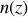, alors
.
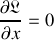La grandeur
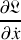est une constante en
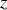: elle est conservée le long de l'axe de propagation, pendant la propagation (voir plus loin la notion de coordonnée cyclique et de loi de conservation).
Cette situation est typique d'une variation d'indice le long de l'axe optique représentée sur le schéma de la Fig. 10.
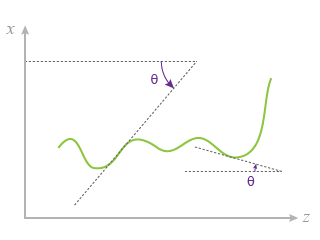
Ainsi pour une trajectoire quelconque
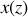du faisceau lumineux, telle celle représentée sur la figure (Fig. 10),
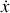caractérise la pente de la tangente et donc
.
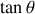Le coefficient
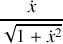n'est rien d'autre que
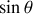, en tout point
.
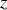Cette relation de 'conservation' est la forme continue de la loi de Snell-Descartes le long de l'axe optique :
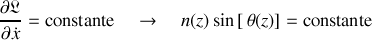
avec toutes les applications qui découlent de cette forme continue de la loi.
2) Si la dépendance en
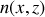est prise en compte, le calcul complet conduit à :
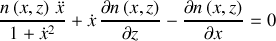
La "conservation" précédente n'existe plus : la variation d'indice, parallèlement à la direction de propagation, contribue à la réfraction selon l'axe de propagation.
En fonction de l'angle
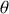dans le plan, cette équation indique une variation d'inclinaison selon la direction de propagation :
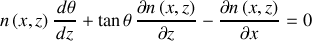
Ainsi tous les cas de réfraction peuvent être déclinés selon les fonctions d'indice expérimentales.
En particulier, avec quelques calculs perturbatifs, les divers phénomènes d'aberration peuvent être mis en évidence.
Outre les développements de l'indice autour de valeurs particulières, une variation continue de l'indice peut expliquer les phénomènes d'optique de type mirages.
La dépendance de l'indice
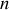selon
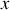modifie la symétrie autour de l'axe de propagation
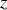et introduit des distorsions lumineuses.
Et tenir compte de l'axe
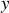et de variations selon cet axe multiplie les dissymétries.
La source produit le plus souvent un fin faisceau, utilisé faiblement incliné par rapport à l'axe de propagation.
Le choix des coordonnées cartésiennes est motivé par la présence de symétries axiales, lesquelles caractérisent essentiellement les éléments optiques placés sur le trajet du faisceau.
La description dans un espace continu permet de suivre la propagation dans un milieu continu. Dans ce cas, la forme du faisceau peut jouer un rôle non négligeable.
