Au vu de sa définition dans la fonctionnelle "action" ou des équations issues de la minimisation de cette dernière, le lagrangien vérifie les propriétés suivantes.

1) Le lagrangien est défini à une constante additive près.

• Les équations du mouvement issues de 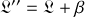décrivent le même système que celui décrit par .

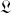  Cette propriété peut être associée à l'énergie potentielle, source du mouvement.

  • Plus remarquable, du fait de la forme des équations d'Euler- Lagrange et surtout du rôle particulier du paramètre continu 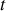, le lagrangien est défini à une fonction du temps près  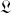: décrit le même système que .

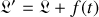Cette propriété permet de simplifier et résoudre certains problèmes non conservatifs, ouverts, reliés à un moteur par exemple.

2) Additivité des lagrangiens.

• Si 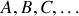sont des systèmes suffisamment distants les uns des autres pour que leurs interactions 2 à 2 soient négligeables à l’ordre dominant, le lagrangien du système total s'écrit .

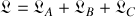  Dans ce cas, les équations sont découplées selon chaque sous-système : le système décrit par 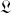est la superposition des 3 autres.

  L'intérêt de cette propriété est encore plus fort car lorsqu'une interaction existe, elle apparaît souvent et d'abord sous forme additive et perturbative, par exemple.

  Son traitement par les équations d'Euler- Lagrange reste additif par rapport aux deux sous-systèmes avec un couplage perturbatif.

3) Dans l'exemple du pendule plan, le passage à une échelle de temps propre au système a mis en évidence l'émergence d'un paramètre multiplicatif au lagrangien.

Le système décrit étant le même, ses solutions sont identiques.

Une troisième propriété est déduite :

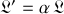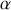• Si , où est une constante réelle, les équations du mouvement pour 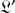sont identiques à celles de .

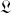  En physique, cette propriété revient à une opération de renormalisation (redéfinition) des paramètres à l'origine de l'interaction, comme la masse du système (unité de mesure), et variables.

  • Mais attention 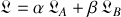ne décrit pas la superposition des deux systèmes décrits par respectivement par 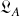et 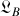sauf si .

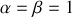    La combinaison linéaire de lagrangiens peut poser le problème de la simultanéité des interactions à l'origine des coefficients, de renormalisations incompatibles.

4) La transformation de jauge :

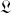• et 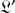décrivent le même mouvement si .

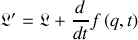Cette dernière propriété permet de définir une famille de problèmes décrits par des lagrangiens qui se déclinent les uns par rapport aux autres à travers les fonctions 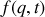et dont les solutions sont identiques.

La dérivée totale s'écrit sous la forme : 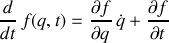; cette dépendance linéaire en la vitesse généralisée prend un sens particulier.

Ainsi dans le cas de l’espace réel à trois dimensions, cette propriété correspond à la transformation de jauge des champs (voir l'exercice d'application).

D'où la dénomination de "transformation de jauge" : 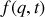est une génératrice de nouvelles fonctionnelles.