On peut également relier la loi de Lenz-Faraday à la force de Lorentz et réciproquement. Ainsi nous avons défini la force électromotrice 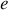régnant entre les bornes 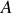et 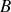infiniment proches d'un circuit fermé 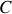comme la force moyenne s'appliquant sur les porteurs de charge (les électrons). Ainsi

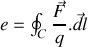
Or la force s'appliquant sur le porteur de charges est la force de Lorentz

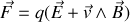
Remarquons que l'on peut introduire un champ 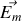homogène à un champ électrique dit champ électromoteur tel que

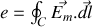
Par identification

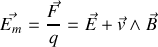
dit champ électromoteur, est le champ électrique vu par l'élément de courant dans le référentiel du laboratoire. Cette forme est particulièrement pratique pour les problèmes tels que le freinage par courants de Foucault. Par la loi de Galilée de composition des vitesses, la vitesse du porteur de charges est la somme de sa vitesse 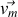par rapport une origine fixe 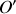du circuit et de la vitesse 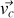du circuit (ou de son origine 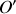) par rapport à l'origine du laboratoire 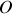. Ainsi

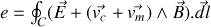
Or la vitesse du porteur de charges 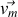est forcément colinéaire à 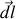élément de longueur du circuit ; par conséquent après application du produit vectoriel avec 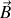sa contribution est nulle et on peut ne garder que 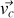. Il reste dans la force électromotrice

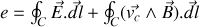
Comparons désormais cette expression avec la loi de Lenz-Faraday reliant 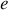au flux du champ magnétique 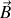à travers la surface 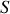du circuit

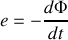
avec

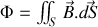
La dérivée est ici une dérivée dite "totale". (dérivant par rapport à une variation explicite du flux par rapport au temps). Si nous décomposons désormais, comme il est courant en mécanique des fluides, cette dérivée en un terme dépendant explicitement du temps (par exemple correspondant au cas où le champ change au cours du temps, ou la surface ou le produit scalaire change), et en un terme dépendant implicitement du temps (dans le cas d'un circuit mobile) nous obtenons ce qui est appelé la dérivée partielle par rapport au temps ainsi qu'un terme dit "convectif" lié au déplacement du circuit :

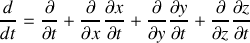
nous reconnaissons les vitesses dans cette expression et finalement

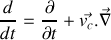
donc

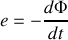
donne

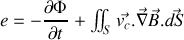
nous pouvons sortir 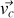de l'intégrale et une application de la formule de Stokes en remarquant que

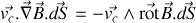
car

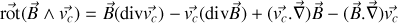
ce qui peut se montrer avec un peu de patience en cartésiennes. Or 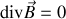; et si nous remarquons de plus que la vitesse 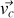est une constante dans l'espace ses dérivées spatiales sont nulles.

Finalement

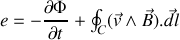
le deuxième terme est identique à celui de l'expression obtenue au début du paragraphe à partir de la force de Lorentz, et correspond à une vitesse éventuelle du circuit par rapport au référentiel d'étude, alors que le premier terme correspond à une induction locale au circuit. Nous identifions alors

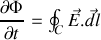
et nous allons voir que l'on peut obtenir une forme locale de cette équation.