En effet, si nous établissons sous forme locale une équation assez intuitive que nous connaissons déjà sous différentes formes, à savoir l'équation de conservation de la charge, nous allons arriver à une incohérence.
Revenons à la définition de la densité de courant
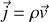
où
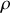est la densité de charges et
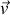leur vitesse.
Si nous considérons un petit tube de charge de volume
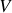, de surface
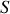perpendiculaire à
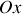et longueur dl suivant
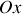, avec
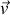uniforme et parallèle à
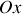(avec
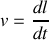) alors la charge totale
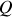présente dans le tube vaut
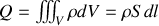
La variation de la charge durant un intervalle de temps
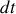est égale à la somme des charges entrantes et sortantes (s'il n'y a pas de création). Comme l'intensité électrique
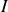sortante vaut
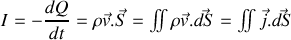
(si le flux sortant est positif la charge dans le volume diminue), en appliquant la formule de Green-Ostrogradski au membre de droite nous obtenons si nous considérons que le volume
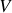est arbitraire et donc que les intégrandes sont égales :
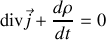
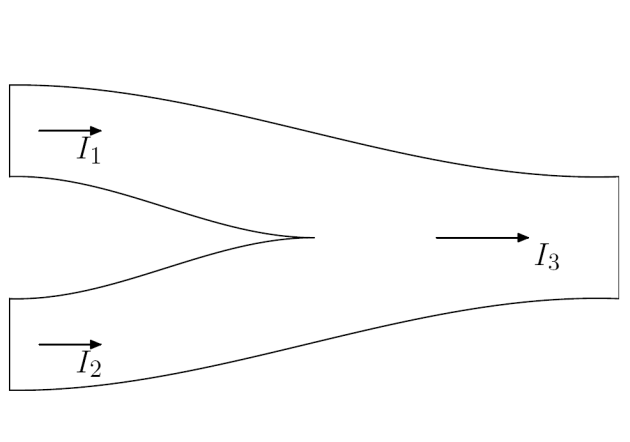
Remarquons que cette équation de conservation de la charge se réduit en régime permanent à
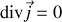
ce qui est par exemple une expression de la loi des noeuds : la somme des intensités entrantes est égale aux intensités sortantes s'il n'y a pas d'accumulation ou de perte locale.
