Comme 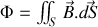une application du théorème de Stokes au membre de droite de l'expression de la dérivée partielle du flux par rapport au temps dans le paragraphe précédent donne

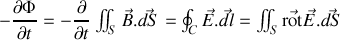
ainsi comme la surface 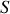est quelconque à partir du moment où elle est enserrée par le circuit 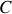il faut que les intégrandes soient égales et donc

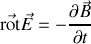
en faisant rentrer la dérivée temporelle sous l'intégrale (nous sommes en physique !). Cette formule locale, obtenue encore une fois à partir d'une loi intégrale (la loi de Lenz-Faraday) est appelée équation de Maxwell-Faraday. Elle relie le rotationnel du champ électrique à ses causes, à savoir une variation du champ magnétique dans le temps. Remarquons qu'en régime stationnaire (indépendant du temps) ce rotationnel du champ électrique est nul ; ainsi, dans le chapitre précédent, nous avions le droit d'écrire le champ électrique comme gradient du potentiel, ce qui ne sera plus forcément le cas.

Si nous nous souvenons que la divergence du champ magnétique 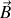est toujours nulle, nous pouvons toujours écrire ce dernier champ comme rotationnel d'un potentiel vecteur

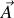
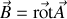
Comme nous venons de trouver l'équation de Maxwell-Faraday

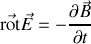
en substituant l'équation pour 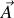on obtient

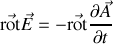
en faisant passer la dérivée temporelle sous le rotationnel. Par conséquent comme le rotationnel d'un gradient est nul les deux expressions sous le rotationnel sont égales à un gradient près ; ce gradient est clairement celui du potentiel électrique pour être cohérent avec le régime stationnaire indépendant du temps

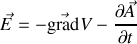
Nous voyons ainsi un terme supplémentaire apparaître dans l'expression usuelle du champ électrique. Cette expression dite champ de Neumann est particulièrement utile dans la recherche des champs émis par une antenne, comme nous le verrons dans une autre partie du cours. Remarquons cependant que ce champ est unique mais qu'on peut changer 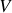et 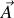simultanément toute en conservant le résultat ( 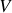est défini à une constante près et 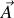à un gradient près). Pour retrouver l'équation de Poisson il nous faut cependant rappeler la condition dite "jauge de Coulomb" telle que

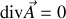
auquel cas on aura toujours

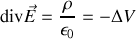
Nous verrons cependant que ce choix pourra poser des problèmes dans les équations de Maxwell dites complètes, avec le "courant de déplacement". On préfère ra alors la jauge dite de Lorentz.