Les formules vues dans les paragraphes précédents sont surtout utiles dans les problèmes concernant une boucle de courant (pour les formules intégrales) ou un dispositif massif tel qu'un barreau conducteur (pour les formules locales). Les dispositifs réels tels que les transformateurs, moteurs, bobinages, etc, sont pourtant souvent à michemin entre ces deux situations, c'est pourquoi il vaut mieux employer des expressions résumant la physique, éventuellement de façon empirique, dans des coefficients globaux.
Ainsi, considérons deux circuits fermés
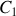 et
et
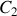 respectivement parcourus par des courants variables
respectivement parcourus par des courants variables
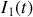 et
et
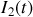 . Le courant
. Le courant
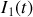 parcourant le premier circuit va créer dans l'espace un champ magnétique
parcourant le premier circuit va créer dans l'espace un champ magnétique
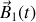 variable qui va induire une force électromotrice dans les deux circuits ; dans le premier circuit on parlera d'auto (ou self) induction et dans le deuxième circuit de mutuelle induction. La réciproque est vraie pour le deuxième circuit.
variable qui va induire une force électromotrice dans les deux circuits ; dans le premier circuit on parlera d'auto (ou self) induction et dans le deuxième circuit de mutuelle induction. La réciproque est vraie pour le deuxième circuit.
Ainsi si nous notons le flux total
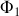 présent dans le premier circuit
présent dans le premier circuit
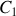 celui-ci se décompose en la contribution
celui-ci se décompose en la contribution
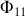 de
de
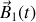 créé par
créé par
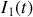 et
et
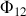 de
de
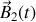 créé par
créé par
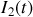
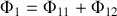
et de même
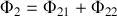
Rappelons que par la loi de Biot et Savart le champ est directement relié à sa cause (le courant) ; ainsi pour
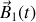 par exemple
par exemple
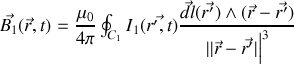
Si nous supposons que l'intensité est constante sur le circuit nous pouvons la sortir de l'intégrale, et si maintenant nous calculons
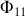 flux de
flux de
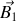 dans
dans
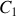
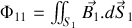
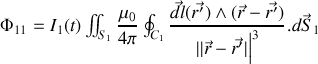
Cette formule effrayante ne doit pas nous cacher que le facteur de droite est simplement géométrique (dépend de l'arrangement mutuel des circuits) et que finalement on peut la résumer sous la forme
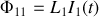
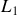 sera appelée auto-inductance du circuit en système international est exprimée en H (Henrys). Souvent sa valeur est plutôt établie expérimentalement que calculée car il y a souvent des "pertes de lignes de champ" qui font que la valeur théorique ne coïncide pas tout à fait avec la valeur expérimentale comme vous pourrez le voir en travaux pratiques.
sera appelée auto-inductance du circuit en système international est exprimée en H (Henrys). Souvent sa valeur est plutôt établie expérimentalement que calculée car il y a souvent des "pertes de lignes de champ" qui font que la valeur théorique ne coïncide pas tout à fait avec la valeur expérimentale comme vous pourrez le voir en travaux pratiques.
Remarquons qu'il faudra bien tenir compte du nombre de spires éventuel dans les calculs de
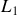 .
.
Ainsi, on va voir apparaître dans le circuit lui-même une force électromotrice s'opposant aux variations du courant le parcourant. Vous avez déjà vu sans doute en électrocinétique de tels dipôles, symbolisés comme par hasard par des bobines et d'impédance
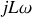 (correspondant à la dérivée de la loi de Lenz) en courant alternatif sinusoïdal.
(correspondant à la dérivée de la loi de Lenz) en courant alternatif sinusoïdal.
Dans certains montages démontrant ce phénomène d'induction mutuelle, on essaiera ainsi de cacher l'auto-induction en choisissant des valeurs de
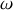 appropriées par rapport aux résistances, aux
appropriées par rapport aux résistances, aux
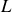 et aux
et aux
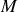 , mais ce phénomène sera toujours présent. En principe il faudrait établir un système de deux équations différentielles couplées pour décrire le phénomène obtenu.
, mais ce phénomène sera toujours présent. En principe il faudrait établir un système de deux équations différentielles couplées pour décrire le phénomène obtenu.
De la même façon nous pouvons établir
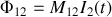
avec
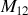 mutuelle inductance des deux circuits, puis
mutuelle inductance des deux circuits, puis
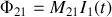
et enfin
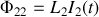
avec comme expression de
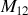
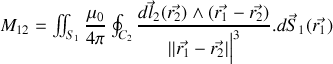
avec
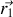 sur
sur
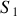 et
et
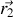 sur
sur
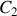 .
.
Si nous remarquons que pour un champ scalaire
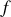 et pour un champ vectoriel
et pour un champ vectoriel
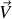
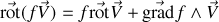
comme
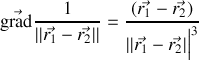
et
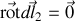
ce qui se démontre trivialement en cartésiennes
il vient
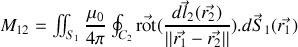
et par une application de la formule de Stokes le rotationnel disparaît
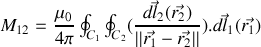
et il reste une formule certes intimidante mais dans laquelle nous pouvons permuter sans encombre les deux indices vu que le signe de la distance
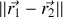 ne changera pas. Ainsi retenons que
ne changera pas. Ainsi retenons que
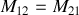
ce que vous pourrez vérifier en travaux pratiques en permutant les bornes des montages démontrant l'induction sans changer le résultat. Retenons que si nous voulons calculer l'auto ou la mutuelle inductance, il faut établir le champ magnétique dans l'espace, puis calculer son flux dans un des circuits, et enfin mettre en facteur l'intensité.




