En régime permanent, les équations déjà obtenues sont cohérentes ; ceci dit, en régime variable, il apparaît une contradiction manifeste entre la forme locale du théorème d'Ampère

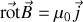
qui implique puisque la divergence d'un rotationnel est nulle

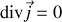
alors qu'en régime variable nous venons de montrer que

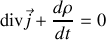
La solution à ce paradoxe proposée par Maxwell est d'introduire un courant fictif supplémentaire nommé courant 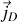de déplacement dans les équations ;

si

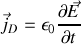
si nous prenons la divergence de la forme locale du théorème d'Ampère avec le nouveau courant 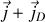il vient

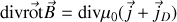
soit, puisque la divergence d'un rotationnel est nulle

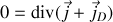
soit encore en employant la conservation de la charge et la définition du courant de déplacement

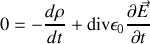
dans la mesure où la forme locale du théorème de Gauss s'écrit

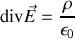
nous arrivons cette fois-ci après simplification algébrique à un membre de droite qui est bien nul et un système d'équations cohérent.

Ce courant de déplacement 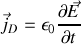apparaît donc en régime variable ; la forme locale du théorème d'Ampère que nous avons établie précédemment reste donc valable en magnéto-statique si les courants sont fixés. Remarquons que comme souvent en physique une avancée théorique n'invalide pas les théories précédentes mais simplement limite leur domaine de validité.

Remarquons d'autre part que si les courants sont lentement variables (approximation dite ARQP pour Approximation des Régimes Quasi-Permanents) on peut négliger le courant de déplacement par rapport aux autres courants et le chapitre précédent sur l'induction reste valable. On peut montrer en exercice que dans les matériaux usuels cette approximation est valable pour des fréquences 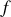inférieures au 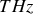et pour des tailles de circuit petites devant la longueur d'onde 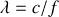, point que nous verrons plus en détail dans le chapitre sur les ondes électromagnétiques.

Figure 4 – Schéma d'un condensateur plan

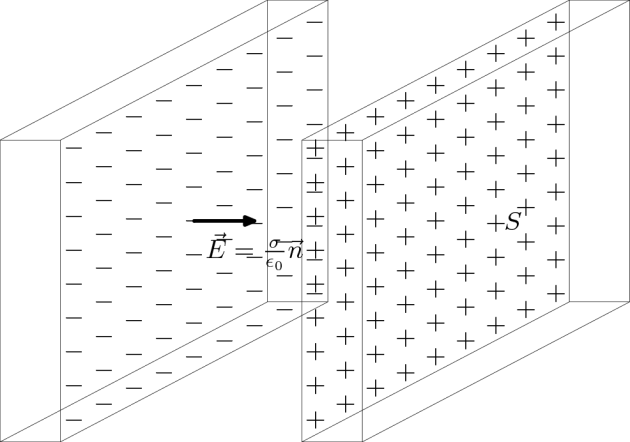
Soit un condensateur idéal formé de deux plaques de surface S chargées 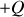et 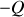éloignées d'une distance 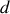dans le vide. Nous avons montré précédemment que le champ est nul à l'intérieur d'un conducteur parfait ; il peut cependant y avoir une densité de charges surfaciques 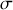, donc ici 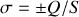. Si nous appliquons les conditions de passage entre l'intérieur et l'extérieur des plaques rappelons que

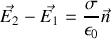
où 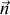est le vecteur normal aux plaques.

Par conséquent puisque le champ est nul dans le conducteur

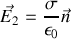
(ce qui permet par ailleurs en intégrant de trouver la valeur de la capacité 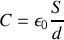du condensateur dans la formule 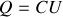avec 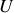différence de potentiel entre les plaques).

Relions maintenant (disons pour 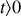) les deux plaques par un conducteur de faible résistance . Le courant "se met à couler" pour équilibrer les charges entre les deux plaques, générant au passage un courant 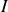. En première approximation si la densité de courant 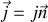est supposée uniforme et normale à la surface

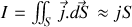
or

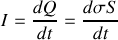
rappelons que nous venons d'établir par les conditions de passage

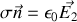
donc en rapprochant les deux équations précédentes 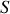disparaît et il reste

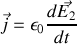
On peut arguer que par continuité du courant, entre les plaques où règne le vide et où donc manifestement il ne peut y avoir de courant on va retrouver la même équation qui est exactement celle que nous avons établie pour le courant de déplacement.

Cet exemple est loin d'être une preuve mais peut contribuer à se convaincre de l'existence de ce courant de déplacement ; il sera d'autant plus intense que la résistance est petite et donc la décharge du condensateur rapide.