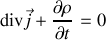Résumons donc le système d'équations corrigé auquel nous arrivons :

-Forme locale du théorème de Gauss dite désormais équation de Maxwell-Gauss (MG)

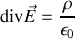
-Forme locale du théorème d'Ampère, corrigée avec le courant de déplacement, dite équation de Maxwell-Ampère (MA)

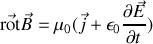
-Forme locale de la loi de Lenz-Faraday, dite équation de Maxwell-Faraday (MF)

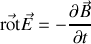
-Conservation du flux magnétique, absence de monopôles magnétiques, dite équation de Maxwell-flux ( )

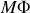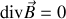
Ces équations sont à connaître par coeur pour tout étudiant en physique dans l'enseignement supérieur.

Remarquons qu'elles ne sont valables que dans le vide ou en présence de charges localisées sans milieu modifiant la valeur des champs. Elles impliquent, comme nous l'avons vu précédemment, l'équation de conservation de la charge électrique