Pour toute transformation quasi-statique d'un système
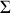échangeant par chaleur avec le monde extérieur
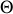la quantité d'énergie
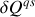, il est loisible d'exprimer la variation différentielle d'entropie de l'Univers i.e. la somme des variations d'entropie de
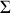et de
:
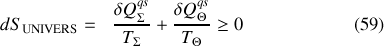
Or, l'énergie perdue ou gagnée par chaleur par l'extérieur (la "source thermique'') est l'opposée de celle gagnée ou perdue par le système :
Par suite, la variation différentielle d'entropie de l'Univers peut s'écrire :
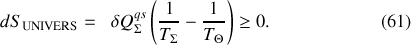
La réversibilité d'une transformation correspondant à une variation nulle de l'entropie de l'Univers, l'équation (61) montre que la réversibilité mécanique et thermique ne peut être atteinte que pour deux transformations différentielles quasi-statiques particulières :
lorsqu'il n'y a pas d'échange thermique (
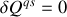)lorsque l'échange thermique a lieu à la même température pour le système et pour le monde extérieur (
).
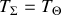Le résultat est identique si, au lieu d'une transformation différentielle, c'est une transformation intégrale qui est considérée. Celle-ci est réversible si elle est adiabatique quasi-statique (
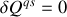en permanence et
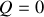) ou si l'échange thermique est tel que, tout au long du chemin suivi, le système et la source thermique restent à des températures égales de part et d'autre (
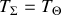). Dans le cas important où la source thermique est un thermostat, l'échange thermique est réversible (
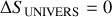) si et seulement s'il est isotherme.
L'inéquation contenue dans (61) montre en outre que si la température du système est plus grande que celle de la source (
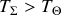) alors le transfert thermique doit se faire du système de référence vers la source (
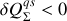). Réciproquement, si elle est plus petite (
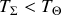) alors le transfert doit se faire vers le système (
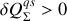). Dans les deux cas, le plus chaud perd de l'énergie par chaleur au profit du plus froid. Le second principe est équivalent au postulat "l''essence de la chaleur [est de] passer des corps chauds aux corps froids'' utilisé par Clausius en 1850 pour démontrer le principe de Carnot.
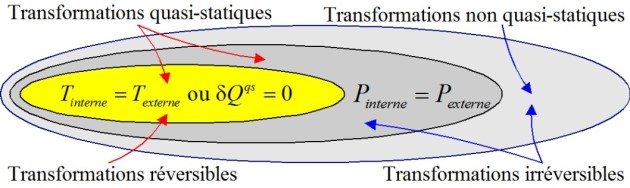
En résumé
un échange d'énergie par travail est mécaniquement réversible (quasi-statique) si la pression intérieure au système et la pression extérieure restent égales au cours de la transformation;
une transformation quasi-statique purement mécanique (adiabatique) est thermiquement réversible, donc réversible;
un échange quasi-statique d'énergie par chaleur est thermiquement réversible, donc réversible, si températures interne et externe au système restent égales au cours de la transformation;
une transformation est réversible si elle est réversible mécaniquement et thermiquement; cela ne se produit qu'en l' absence de chocs et de discontinuités mécaniques ou thermiques.
Remarque :
Une transformation adiabatique quasi-statique est nécessairement isentropique et ne modifie pas l'entropie de l'Univers. "Quasi-statique'' et "réversible'' sont ici rigoureusement équivalents. Cependant, si une adiabatique réversible est isentropique, une isentropique n'est pas obligatoirement adiabatique. Un système peut en effet revenir à son entropie initiale après variation de son entropie au cours de la transformation. Celle-ci est alors isentropique mais pas adiabatique quasi-statique.
