Considérons à nouveau l'interaction thermique entre deux corps A et B séparés par une cloison rigide et diatherme, et isolés du milieu extérieur.

Soien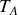t et , et 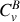les températures initiales et les capacités thermiques de A et B, respectivement. Soit 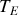la température du système A+B à l'équilibre thermique. Comme les volumes A et B ne varient pas, les variations d'énergie interne et d'entropie de A et B ne dépendent que des variations de température. Que X désigne A ou B, il vient :

Le système A+B étant isolé, son énergie interne se conserve :

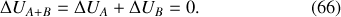
De la résolution de cette équation découle une température d'équilibre

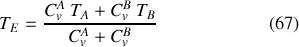
qui constitue le barycentre des températures affectées des "masses'' que sont les capacités thermiques des deux corps A et B et permet de calculer la variation d'entropie du système A+B, soit celle de l'Univers :

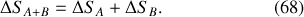
Dans le cas particulier où les deux corps ont une même capacité thermique 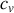, il vient :

et une variation d'entropie de l'Univers simplement égale à :

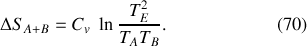
Après utilisation de l'identité remarquable

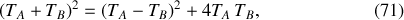
il apparaît que la variation d'entropie de l'Univers se présente sous la forme explicitement positive (ou nulle dans le cas trivial où les températures initiales 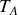et sont égales)

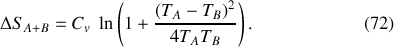
Cela confirme que l'interaction thermique entre deux systèmes à des températures distinctes est nécessairement irréversible. Aisément généralisable, cet exemple permet de mieux comprendre pourquoi un système isolé initialement en déséquilibre thermique va évoluer à la fois vers une température barycentrique uniforme et une entropie maximale. Il suffit pour cela de le diviser par la pensée en petits sous-systèmes, de températures quasi-uniformes mais distinctes.

Considérons un thermostat (système de très capacité thermique susceptible d'échanger de l'énergie par chaleur sans que sa température n'en soit affectée) et le système de capacité thermique .

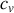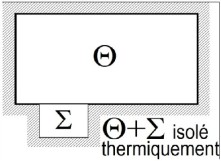
Dès lors que le système interagit thermiquement avec le thermostat , sa température évolue à partir d'une valeur initiale 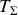jusqu'à la température 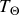du thermostat. De plus, l'ensemble formé par le thermostat et le système étant isolé thermiquement, les quantités d'énergie échangées par chaleur se compensent :

Les variations d'énergie interne et d'entropie du thermostat sont :

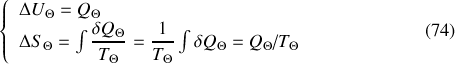
ce qui, en fonction de l'égalité (73) peut être réécrit sous la forme :

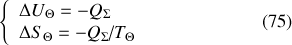
Le système n'échangeant pas de travail avec un opérateur extérieur à l'ensemble ( ),

Les variations d'entropie de et du thermostat sont respectivement :

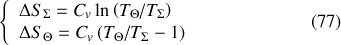
La variation d'entropie de l'Univers due à l'interaction thermique est par conséquent :

Or, il est aisé de démontrer que la fonction 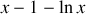est strictement positive, sauf en où elle est nulle. Ce cas particulier correspond à la situation triviale où le système est initialement déjà à la température du thermostat. Dans le cas plus intéressant où et ne sont pas initialement à la même température, l'entropie de l'Univers augmente, ce qui correspond à nouveau à une interaction thermique irréversible.

Hormis le fait de présenter le calcul de la variation d'entropie d'un thermostat idéal, l'exemple précédent n'apporte rien de plus que le premier. Cependant, il permet d'aborder de plain pied une configuration théorique plus originale. 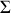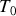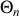Considérons pour ce faire un troisième et dernier exemple, où le système , initialement à la température , est mis en contact thermique avec une succession de thermostats (où l'indice n est compris entre un et N ) affectés de températures 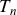telles que :

Parce que tend spontanément vers l'équilibre thermique, sa température augmente à chaque fois de la quantité . Après avoir été mis en contact avec le thermostat 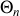, le système est à la température 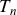. Il entre alors en contact avec 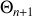et sa température s'élève à 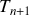. Si est très grand, on peut confondre avec une quantité différentielle , et les variations d'entropie de et de 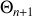consécutives à l'échange thermique sont respectivement:

Il apparaît alors que la variation d'entropie de l'Univers ( 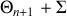) est nulle. Ici, l'échange thermique est réversible. Mais cette réversibilité n'est possible que parce que les températures 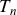et 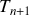sont très proches. Autrement dit, il y a réversibilité parce que l'interaction thermique est isotherme (les deux systèmes 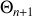et échangent par chaleur tout en étant quasiment à la même température). En multipliant les sources thermiques intermédiaires pour modifier la température d'un corps par des moyens uniquement thermiques, un opérateur diminue donc le caractère irréversible qui accompagne normalement cette modification.