Soit un système 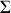qui n'échange que du travail 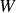avec le milieu extérieur. Un tel système est dit "adiabatique'' ou bien "source de travail''. Quant au milieu extérieur, il consiste en un "opérateur'' M (c'est un machiniste qui donne ou récupère du travail). De façon symbolique, 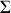peut être représenté par un gaz contenu dans un cylindre thermiquement isolé et clos par un piston. Ce piston est relié à l'opérateur M.

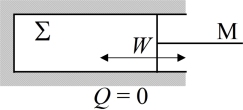
La variation d'entropie de l'Univers accompagnant un échange de travail entre 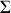et M est égale à la somme de la variation d'entropie du système adiabatique 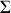et de celle de l'opérateur M, mais la variation d'entropie de M est nulle.

Par suite, d'après le 2^nd principe :

Ainsi, alors même qu'aucun échange de chaleur ne se produit, l'entropie d'un système adiabatique augmente si la transformation est irréversible. Selon une terminologie du XIX^ème siècle, l'irréversibilité induit une "chaleur interne'' 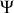. Cette notion de chaleur interne renvoie au concept de "dégradation de l'énergie'' (de travail en chaleur) qui fut alors très utilisé.

Plaçons nous maintenant dans le cas d'une détente ou d'une compression adiabatique non quasi-statique ( 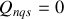). La variation d'énergie interne due à cette transformation est :

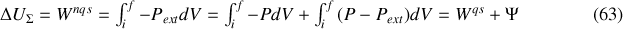
Quant à la variation d'entropie, elle se calcule sur le chemin quasi-statique équivalent :

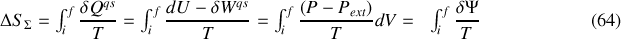
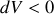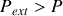Si l'adiabatique n'est pas quasi-statique, qu'elle soit compression ( et ) ou détente ( 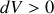et 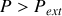), la quantité 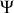est positive. Cela montre qu'une transformation quasi-statique "équivalente'' , permettant à partir du même état initial d'aboutir au même état final, ne serait pas adiabatique et nécessiterait un transfert thermique vers le système 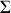. De plus, la variation 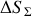étant positive, il en est de même pour l'Univers. L'adiabatique non quasi-statique est bien irréversible.