Quelle est la structure du noyau et quelles sont les forces qui la maintiennent ? Il est difficile de répondre à cette question avec une relative certitude alors que par contre, la théorie atomique des électrons apparaît maintenant bien établie. Cela tient essentiellement à notre ignorance sur la nature des forces qui agissent à très courte distance à l'intérieur du noyau .
Une première explication sera apportée à cette question par le biais de la notion de l'énergie de liaison par nucléon dans un noyau. On prend l'Hydrogène comme exemple porteur du développement de l'argumentation qui suit.
L'Hydrogène possède trois isotopes :
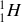 Hydrogène qui ne contient pas de neutrons
Hydrogène qui ne contient pas de neutrons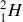 Deutérium qui contient un neutron
Deutérium qui contient un neutron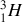 Tritium qui contient deux neutrons
Tritium qui contient deux neutrons
On peut générer le Deutérium grâce au bombardement de l'Hydrogène par des neutrons, réaction décrite par la relation suivante :
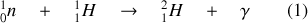
On va pouvoir constater qu'il y a un défaut de masse dans cette réaction. (Voir le cours "Equivalence masse énergie et unités d'énergie en physique nucléaire" pour une introduction à l'égard de l'équivalence masse énergie, les unités d'énergie en physique nucléaire et la notion de défaut de masse).
Les masses en jeux dans cette réaction sont les suivantes :
Masse de neutron

Masse de proton

Somme des deux masses
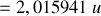
Par ailleurs, nous savons que la masse du noyau de Deutérium au repos , qui consiste d'un proton et d'un neutron = masse de l'atome de Deutérium − masse de l'électron
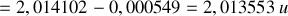
La différence est un défaut de masse de
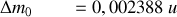
Puisque cette masse est au repos elle vaut par la théorie de relativité une énergie :
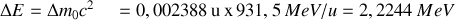
Cette énergie manquante au noyau est perdue sous forme d'une radiation
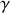 émise vers le milieu extérieur ; voir l'équation (1). Cette énergie manquante peut être considérée comme le puits de potentiel dans lequel les deux nucléons, le proton et le neutron, sont maintenant internés au noyau. Une image thermodynamique est peut être utile (mais pas quantitative !) : dans la réaction, le système perd de l'énergie vers l'extérieure à tel point qu'il gèle.
émise vers le milieu extérieur ; voir l'équation (1). Cette énergie manquante peut être considérée comme le puits de potentiel dans lequel les deux nucléons, le proton et le neutron, sont maintenant internés au noyau. Une image thermodynamique est peut être utile (mais pas quantitative !) : dans la réaction, le système perd de l'énergie vers l'extérieure à tel point qu'il gèle.
Dans ce cas on peut parler d'une énergie de liaison par nucléon , (qui assure leur internement), en divisant l'énergie de défaut de masse par le nombre de nucléon en question. L'énergie de liaison par nucléon pour le noyau de Deutérium est donc :
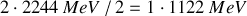 .
.
Attention :
Une question majeure s'impose : Est ce que cette énergie de liaison par nucléon, calculé par exemple pour le noyau du Deutérium, est une constante universelle pour tous les nucléons de tous les noyaux et isotopes ? La réponse s'avère négative.
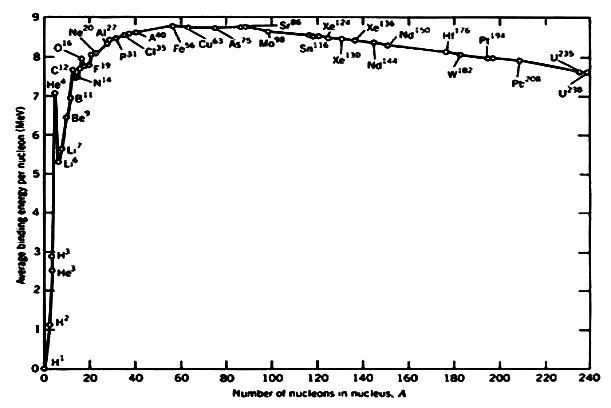
On peut construire en effet une courbe de la variation de cette énergie de liaison par nucléon pour les divers noyaux et isotopes. Cette courbe présentée dans la Fig. 13 comme fonction du nombre de masse
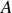 croissant, est obtenue en divisant pour chaque isotope l'énergie totale d'internement des nucléons du noyau par leur nombre dans le noyau.
croissant, est obtenue en divisant pour chaque isotope l'énergie totale d'internement des nucléons du noyau par leur nombre dans le noyau.
L'énergie de liaison par nucléon la plus importante revient au
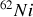 , bien que le championnat de cette énergie soit souvent attribué au
, bien que le championnat de cette énergie soit souvent attribué au
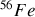 . Les quatre noyaux disposant des énergies de liaison par nucléon les plus élevées
sont comme suit :
. Les quatre noyaux disposant des énergies de liaison par nucléon les plus élevées
sont comme suit :
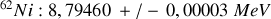
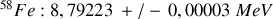
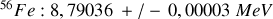
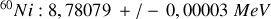
La courbe de la variation de l'énergie de liaison par nucléon pour les isotopes, montre dans la Fig. 13, pour
 , plusieurs pics qui correspondent en fait aux noyaux de
, plusieurs pics qui correspondent en fait aux noyaux de
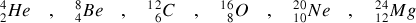
Le noyau
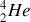 (particule alpha), est particulièrement stable. Les autres noyaux dans cette série sont en effet des multiples du noyau
(particule alpha), est particulièrement stable. Les autres noyaux dans cette série sont en effet des multiples du noyau
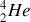 , ce qui peut expliquer leur grande stabilité sous guise d'ensemHebles de particules alpha.
, ce qui peut expliquer leur grande stabilité sous guise d'ensemHebles de particules alpha.
Remarque :
Le fait que la courbe de la Fig. 13 présente un sommet dans la région de grande stabilité de l'élément de Fer, conduit à une conclusion significative à l'égard de l'énergie nucléaire.
Complément :
En effet, il y a libération d'énergie lorsqu'on réussit à casser un noyau lourd en deux noyaux plus légers, ceci s'appelle la fission. Il y a aussi libération d'énergie lorsqu'on réussit à fusionner en réaction nucléaire deux noyaux légers pour constituer un noyau lourd, ceci s'appelle la fusion. Les énergies de liaison par nucléon étant de quelques
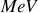 , les énergies libérées dans ces réactions nucléaires sont très supérieures aux énergies libérées dans des transitions optiques atomiques qui se mesurent en
, les énergies libérées dans ces réactions nucléaires sont très supérieures aux énergies libérées dans des transitions optiques atomiques qui se mesurent en
 .
.
Voir la Fig. 14 pour la carte des masses d'isotopes en unités atomique
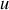 , avec les limites de nos connaissances dans ce domaine en termes de marges d'erreur. Vous pouvez également consulter la référence bibliographique pour des valeurs numériques précises de ces masses, en
, avec les limites de nos connaissances dans ce domaine en termes de marges d'erreur. Vous pouvez également consulter la référence bibliographique pour des valeurs numériques précises de ces masses, en
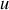 .
.
Exemple :
La fission du Plutonium
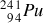 se fait par bombardement par neutrons selon l'équation :
se fait par bombardement par neutrons selon l'équation :
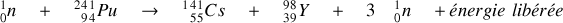
Curieusement un des produits de l'interaction sont trois neutrons. Pour déterminer en
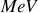 la valeur de l'énergie libérée lors de cette fission du noyau du Plutonium, il faut calculer le bilan de nombre de masse de cette réaction. Dans cette réaction
la valeur de l'énergie libérée lors de cette fission du noyau du Plutonium, il faut calculer le bilan de nombre de masse de cette réaction. Dans cette réaction
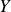 et
et
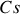 représentent les éléments d'Yttrium et de Césium.
représentent les éléments d'Yttrium et de Césium.
Il y a un défaut de masse :
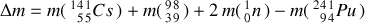
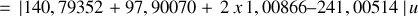
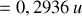
Ainsi l'énergie libérée
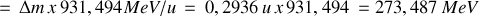
On dit parfois qu'une réaction de ce type peut donner une réaction en chaine. Pouvez-vous justifier ce terme ?
Exemple :
La fusion du Deutérium et de Tritium donne lieu à la réaction nucléaire suivante
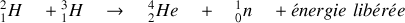
Il y a un défaut de masse
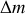 qui vaut en
qui vaut en
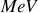
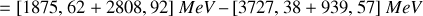
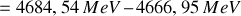
Ainsi l'énergie libérée
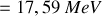
On constate que le rendement énergétique fractionnel de cette fusion est de 17,59 / 4684,54 = 0,00375 par masse. Vérifier que le rendement énergétique fractionnel de la réaction de fission de l'Exemple précédent peut s'écrire en unités de
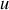 comme 0,2936 / 242,0138 = 0,00121.
comme 0,2936 / 242,0138 = 0,00121.




