La construction d'un noyau atomique revient à construire un assemblage contenant des protons et des neutrons. On a déjà vu auparavant une série de noyaux qui présentent une grande stabilité pour
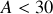, à savoir :
,
,
,
,
,
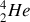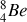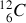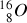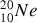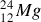. Ce qui est notable dans cette série est le fait que le nombre de protons
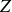soit égal au nombre de neutrons
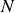. Ceci s'avère un critère de stabilité pour les petits nombres de masse
.
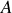Plus particulièrement on observe que les noyaux stables sont ceux qui ont un nombre
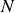égal ou légèrement supérieur au nombre
.
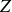Exemple :
Les noyaux :
,
,
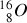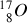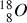sont stables (ils présentent de très longues mi-vies),
mais
les noyaux :
,
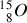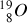ne sont pas stables (ils présentent de courtes mi-vies).
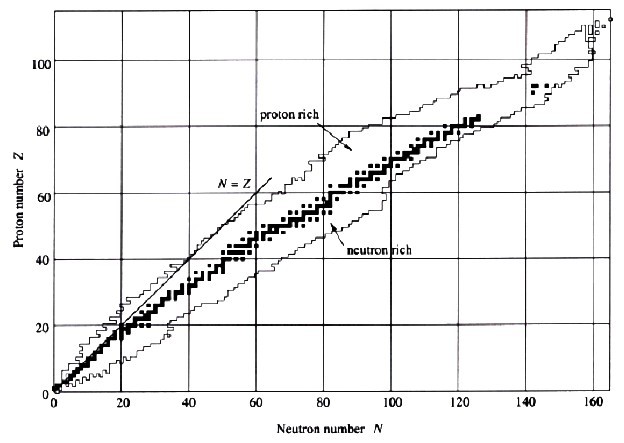
On constate sur la carte de la figure 18 des durées de mi-vie très longues pour certains isotopes :
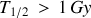(Giga années) indiqués en noir. Par ailleurs la violet, par exemple, correspond à des mi-vies de :
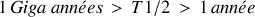. Pour approfondir cette question de stabilité, les isotopes de grande stabilité sont présentés dans la Fig. 19.
Remarque :
Pour les petits nombres de masse
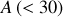, la condition de stabilité est d'avoir
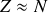comme explicité auparavant. Il est couramment admis que cette situation est probablement due au fait que lorsque
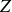est petit, l'énergie potentiel coulombienne due aux protons, stockée au noyau, est basse ce qui permet aux protons et neutrons de peupler des niveaux énergétiques accessibles d'une manière équilibrée, indépendamment les uns des autres.
Exemple :
Dans l’exemple actuel il est utile d’estimer l’énergie d’anti-liaison par proton de 2 protons confinés dans le même volume.
Deux protons internés ensemble se trouvent dans un noyau quasi sphérique. S’excluant mutuellement, on peut estimer la distance
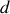entre leurs centres de masse comme deux fois leur rayon. Considérant le rayon d’un nucléon comme
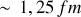, on a donc
.
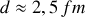L'énergie potentielle coulombienne stockée par l'interaction des deux protons peut s'écrire dans une formulation classique comme :
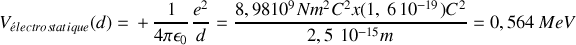
Il s'ensuit que l'énergie d'anti-liaison par proton est de
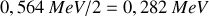, valeur qui n'est pas complètement négligeable devant celle de l'énergie de liaison par nucléon.
Cependant, pour les noyaux lourds avec grand
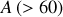, cette énergie coulombienne, positive, s'ajoute au puits de potentiel de nucléons neutres, (voir le calcul de l'Exemple de l'équation 5) ; elle augmente avec le nombre de protons
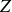, poussant leurs niveaux énergétiques vers le haut. La Fig. 20 présente schématiquement les puits de potentiel de neutrons (à gauche) et de protons (à droite) du
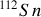, montrant ce décalage vers le haut du potentiel de protons et ses niveaux énergétiques calculés par modélisation en mécanique quantique dus au S.G. Nilsson.
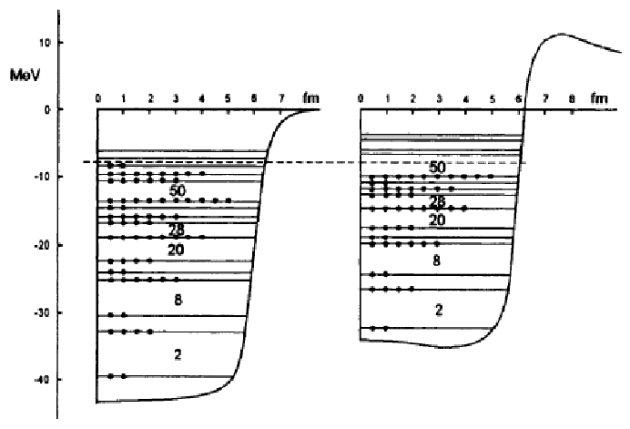
Pour minimiser l'énergie du système avec
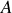croissant, ce qui est une condition nécessaire pour la stabilité du noyau, le système préfère peupler ses nucléons
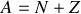avec
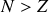. Cette analyse explique la tendance de la dite vallée de stabilité, (suivant les carrés noirs de la Fig. 19), à courber de
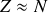à petits
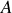vers la condition de
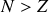à grand
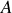. Une représentation topographique
à trois dimensions pour
,
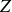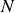et
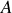est présentée par la Fig. 21.
Remarque :
Enfin les noyaux sont particulièrement stables quand ils possèdent certains nombres dits magiques, de protons ou de neutrons : 8, 20, 28, 50, 82, 126, 184, nombres dont l'origine est à peu près, mais pas complètement, comprise. Les noyaux qui ont à la fois un nombre de neutrons et un nombre de protons égaux à l'un des nombres magiques sont dits doublement magiques, et sont particulièrement stables. C'est par exemple le cas du
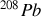qui est constitué de 82 protons et 126 neutrons.
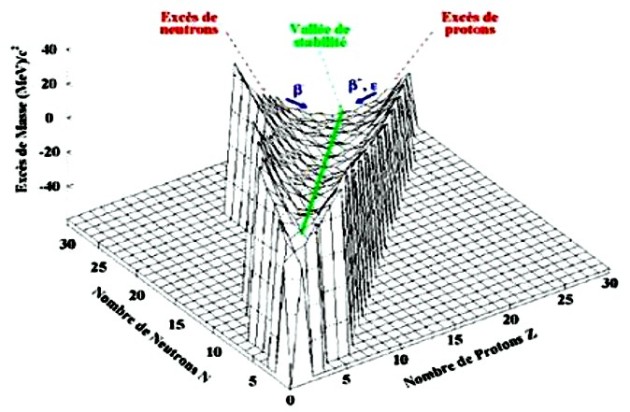
Le début de la vallée de stabilité aves les processus de radioactivité favorisés de part et d'autre via les émissions de
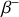et en
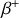des noyaux de neutrons et de proton, respectivement
