Attention :
Les noyaux sont constitués de protons et de neutrons. Il est donc important de connaître les forces qui assurent leur cohésion au sein des noyaux atomiques. L'argument d'un puits de potentiel via l'énergie de liaison qui assure leur internement au noyau est utile et relativement quantifié, mais en tout cas devrait être raffiné.
Les expériences de diffusion de particules élémentaires sur les noyaux, dans des conditions diverses et pour des énergies d'incidence variées, sont une source d'informations très importante. L'expérience la plus facile est celle qui consiste à diffuser des protons (projectiles de sonde) sur des protons (cibles). A grande distance, et ici cela signifie des distances de l'ordre de
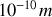 à
à
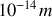 , la force de répulsion coulombienne gouverne l'interaction entre ces protons chargés. On peut démontrer que la formule de diffusion de Rutherford du cours "Formule de section efficace de diffusion de particules alpha" s'applique à ces distances pour le cas de la diffusion proton – proton, puisque la force d'interaction est de la loi de l'inverse carré.
, la force de répulsion coulombienne gouverne l'interaction entre ces protons chargés. On peut démontrer que la formule de diffusion de Rutherford du cours "Formule de section efficace de diffusion de particules alpha" s'applique à ces distances pour le cas de la diffusion proton – proton, puisque la force d'interaction est de la loi de l'inverse carré.
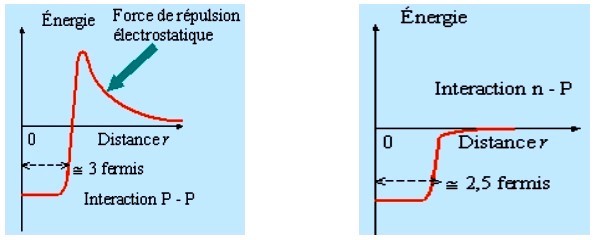
Cependant, à très courte distance, de l'ordre de
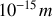 (
(
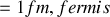 ), apparaît une force nucléaire forte d'attraction proton − proton et proton − neutron, nettement supérieures aux forces de répulsion coulombiennes. Les Fig. 15 ci-jointes dressent schématiquement la combinaison de deux idées de base. D'abord un puits de potentiel apparaît assurant l'internement de deux nucléons, qu'ils soient protons ou neutrons. Deuxièmement le potentiel d'interaction proton – proton diffère du potentiel proton – neutron par la conjugaison de la force d'attraction nucléaire, active à l'échelle du rayon du nucléon, avec la force de répulsion coulombienne active à plus grandes distances. On verra plus tard que le rayon d'un nucléon est
), apparaît une force nucléaire forte d'attraction proton − proton et proton − neutron, nettement supérieures aux forces de répulsion coulombiennes. Les Fig. 15 ci-jointes dressent schématiquement la combinaison de deux idées de base. D'abord un puits de potentiel apparaît assurant l'internement de deux nucléons, qu'ils soient protons ou neutrons. Deuxièmement le potentiel d'interaction proton – proton diffère du potentiel proton – neutron par la conjugaison de la force d'attraction nucléaire, active à l'échelle du rayon du nucléon, avec la force de répulsion coulombienne active à plus grandes distances. On verra plus tard que le rayon d'un nucléon est
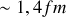 faisant d'un couple de nucléons un puits de potentiel de largeur
faisant d'un couple de nucléons un puits de potentiel de largeur
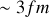 .
.
Remarque :
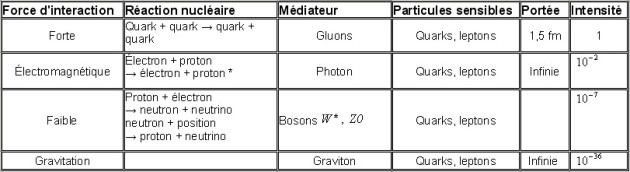
La force nucléaire forte est, avec la force de gravitation, la force électromagnétique, et la force nucléaire faible, une des quatre interactions fondamentales de la physique.
La force nucléaire forte est 100 à 1 000 fois plus forte que la force électromagnétique : elle agit comme une glue à l'intérieur des atomes, maintenant les protons et les neutrons confinés dans le noyau. Ces protons et ces neutrons sont eux-mêmes composés de particules encore plus élémentaires : les quarks, qui sont également retenus grâce à la force nucléaire forte. La force nucléaire faible est très peu intense : elle est environ 100 000 fois plus faible que la force nucléaire forte. Elle est notamment responsable de la radioactivité provoquant la rupture ou la mutation du noyau, alors que la force forte maintient l'unité du noyau.
La question qui se pose ensuite est naturellement : Comment développer une analyse quantitative du noyau et de sa forme matérielle ?
Les expériences de diffusion de particules chargées par des noyaux suivent la loi de l'interaction coulombienne pourvu que ces interactions passent à des distances supérieures à
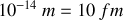 . On peut donc penser que le rayon nucléaire est au plus égal à cette valeur.
. On peut donc penser que le rayon nucléaire est au plus égal à cette valeur.
On peut analyser les dimensions de la forme nucléaire plus directement et avec plus de précision en faisant diffuser par les noyaux de neutrons cinétiquement très énergétique. Les neutrons ne sont pas soumis à la force coulombienne qu'elle soit positive ou négative. Ils ne sont déviés ou absorbés donc que s'ils s'approchent à une distance très courte du noyau. Etant une particule quantique, le neutron présente une longueur d'onde de
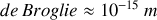 pour une énergie cinétique du neutron à
pour une énergie cinétique du neutron à
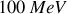 .
.
Conseil :
Pour accompagner ces expériences il faut développer une théorie de diffusion quantique appropriée car la théorie classique de diffusion de Rutherford n'est plus applicable.
On peut démontrer ainsi grâce aux résultats expérimentaux de diffusion de neutrons, comparés avec la modélisation théorique, que le rayon nucléaire
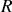 est lié au nombre de masse
est lié au nombre de masse
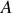 par la relation :
par la relation :
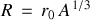 , où
, où
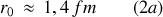
Notons la racine 1/3 sur
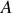 dans l'équation ; le rayon le plus gros noyau connu (avec le plus grand
dans l'équation ; le rayon le plus gros noyau connu (avec le plus grand
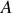 ), ne dépasse pas
), ne dépasse pas
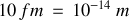 !
!
La même expérience de diffusion conduite avec des électrons ayant une énergie cinétique de
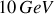 (dont la longueur d'onde de
(dont la longueur d'onde de
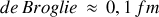 ) conduit à la même relation mais avec un paramètre caractéristique
) conduit à la même relation mais avec un paramètre caractéristique
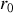 légèrement différent :
légèrement différent :
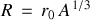 , où
, où
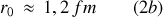
On peut transformer les équations (2a) et (2b), linéaires en R, en une équation pour couvrir la sphère (ou la quasi-sphère) du noyau comme suit :
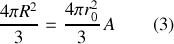
Le premier terme à gauche de l'équation (3) est le volume de la sphère nucléaire, tandis que le seconde terme
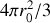 mesure le volume d'un nucléon. Cette équation renseigne dans sa forme simple que le volume du noyau pourrait être interpréter comme le volume du nucléon multiplié par le nombre de masse
mesure le volume d'un nucléon. Cette équation renseigne dans sa forme simple que le volume du noyau pourrait être interpréter comme le volume du nucléon multiplié par le nombre de masse
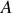 . L'argumentation qui suit confirme cette image. Compte tenu de la forme d'équation (3) pour le volume de la sphère nucléaire et le résultat de l'exemple qui suit, la densité de matière nucléaire est reconnue comme constante.
. L'argumentation qui suit confirme cette image. Compte tenu de la forme d'équation (3) pour le volume de la sphère nucléaire et le résultat de l'exemple qui suit, la densité de matière nucléaire est reconnue comme constante.
Attention :
La densité nucléaire, qui est en effet de l'ordre de
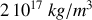 , est nettement supérieure à toute autre densité de la matière. Ces valeurs conduisent à supposer que les densités de nucléons et de charge dans le noyau soient relativement homogènes.
, est nettement supérieure à toute autre densité de la matière. Ces valeurs conduisent à supposer que les densités de nucléons et de charge dans le noyau soient relativement homogènes.
Exemple :
Dans cet exemple on montre que la densité de masse nucléaire et la densité de charge nucléaire sont homogènes au coeur du noyau.
Posons la densité de masse nucléaire comme

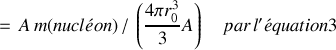
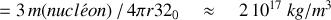
Posons ensuite la densité de charge nucléaire comme
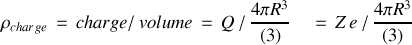
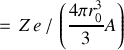
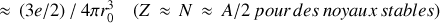
Il s'ensuit que
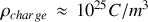 .
.
Puisque les interactions nucléaires fortes dans le noyau existent seulement à très courtes distances
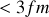 , (avec une énergie de liaison assez importante de l’ordre de quelques
, (avec une énergie de liaison assez importante de l’ordre de quelques
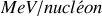 ), et puisque les rayons des nucléons sont dans une fenêtre de
), et puisque les rayons des nucléons sont dans une fenêtre de
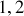 à
à
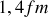 , on peut en déduire que les interactions via la force nucléaire forte entre les nucléons n’existent qu’entre les nucléons qui se touchent. Ceci conduit à une image d’empilement compact de sphères, avec au plus 12 nucléons entourant chaque nucléon au coeur du noyau. Cette image conduit par ailleurs à distinguer un nucléon au coeur du noyau d’un noyau à la surface avec moins de voisins. Si cette image convient pour les nucléons, les forces répulsives coulombiennes cependant entraînent que chaque proton interagit avec tous les protons du noyau, cette force électrostatique devenant de plus en plus importante pour les noyaux lourds avec un nombre croissant de protons.
, on peut en déduire que les interactions via la force nucléaire forte entre les nucléons n’existent qu’entre les nucléons qui se touchent. Ceci conduit à une image d’empilement compact de sphères, avec au plus 12 nucléons entourant chaque nucléon au coeur du noyau. Cette image conduit par ailleurs à distinguer un nucléon au coeur du noyau d’un noyau à la surface avec moins de voisins. Si cette image convient pour les nucléons, les forces répulsives coulombiennes cependant entraînent que chaque proton interagit avec tous les protons du noyau, cette force électrostatique devenant de plus en plus importante pour les noyaux lourds avec un nombre croissant de protons.
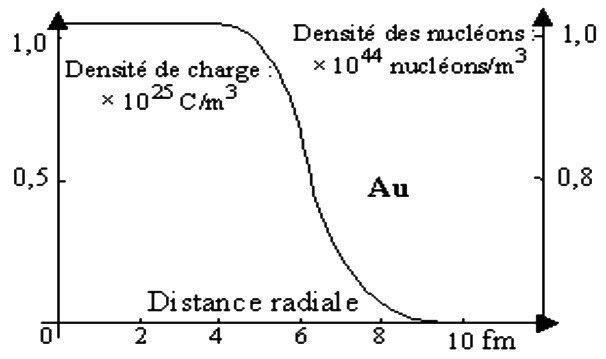
Le noyau n'a pas vraiment de surface abrupte comme un ballon. Les protons et neutrons se déplacent à l'intérieure du noyau conformément à la probabilité spatiale de leurs positions déterminée en mécanique quantique, ce qui donne forme à la graphique de Fig. 16. Il est donc d'usage de définir le rayon effectif
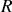 du noyau comme la distance radiale entre le centre du noyau et une surface sphérique imaginaire se trouvant à un rayon
du noyau comme la distance radiale entre le centre du noyau et une surface sphérique imaginaire se trouvant à un rayon
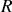 où, par convention la densité à cette surface est la moitié de la densité au centre :
où, par convention la densité à cette surface est la moitié de la densité au centre :
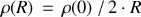 correspond au point d'inflexion de la courbe dans cette région.
correspond au point d'inflexion de la courbe dans cette région.
Remarque :
La figure 16 montre une transition de la matière du noyau vers l'extérieure qui se fait sur une région intermédiaire appelée la surface du noyau.
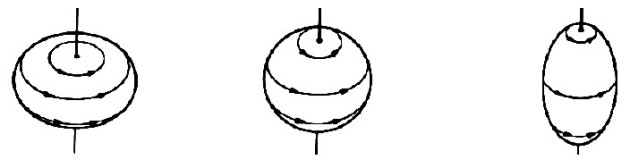
Enfin, les graphiques présentées dans la Fig. 16 n’impliquent pas nécessairement que le noyau soit parfaitement sphérique. Des résultats expérimentaux de diffusion montrent, en effet, en mesurant le moment électrique quadripolaire des noyaux, qu’en leur majorité les noyaux ont plutôt la forme d’un ellipsoïde de révolution. La Fig. 17 illustre ainsi les possibilités des formes observées pour les noyaux : oblate, sphérique et prolate.