Pourquoi une relation pour l'énergie de liaison par nucléon
?
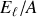On a vu que l'énergie de liaison par nucléon n'est pas une constante universelle, mais varie avec les noyaux et isotopes selon la forme de la Fig. 13. Il est donc utile de comprendre le pourquoi de cela pour accéder à une compréhension plus approfondie de la nature et le fonctionnement des forces nucléaires qui tiennent le noyau en une seule pièce, en formats parfois stables mais souvent instables et radioactifs.
La première étape est évidemment de bâtir un schéma, certes empirique, pour décrire d'une manière succinct l'ensemble des résultats pour les énergies de liaison
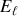de tous les isotopes. Ceci permettrait une vision globale de la déclinaison de cette énergie en termes de ses principales composantes et préparerait une première compréhension en avançant vers une modélisation théorique plus approfondie de forces nucléaires. Développée par C.F. von Weizsäcker et H. Bethe en 1935, ce modèle théorique simple est basé sur l'idée que le noyau se comporte comme une goutte de liquide incompressible.
Ainsi on construit l'énergie de liaison
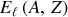pour les noyaux
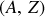en additionnant plusieurs contributions simples comme suit.
L'énergie de volume du noyau
Excepté certains nombres de masse
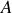, l'énergie de liaison est approximativement proportionnelle à ce nombre ; cette première importante contribution est comptabilisée donc par le terme :
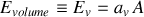
L'énergie de surface du noyau
Cette contribution est nécessairement proportionnelle à la surface du noyau sphérique et par conséquent au rayon carré
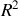; puisque les nucléons à la surface sont moins tenus que ceux enfouis à l'intérieur du noyau, car ils ont moins de voisins, cette contribution serait négative et est comptabilisée, vu les équations 2a et2b, par le terme :
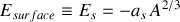
L'énergie électrostatique du noyau
De nature coulombienne, elle est nécessairement proportionnelle à la charge totale
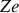stockée par le noyau ; on peut démontrer qu'une sphère chargée d'une façon homogène possède une énergie électrostatique proportionnelle au produit
et inversement proportionnelle au rayon de la sphère
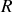. Puisque les autres contributions ont pour rôle de maintenir les nucléons ensemble, à l'inverse de la contribution coulombienne qui voudrait les disperser, cette contribution aura un signe négatif ; elle est donc comptabilisée par le terme :
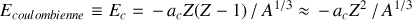
Remarque :
Les quatrièmes et cinquièmes terme de ce modèle représentent des contributions à l'énergie de liaison par nucléon, sont issues des effets quantiques.
L'énergie d'asymétrie en N et Z
Ce quatrième terme d'effet d'asymétrie décrit la différence en énergie pour un noyau dont
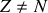et pour le même noyau pour qui les nombres de protons et neutrons,
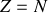. Calculer la différentielle d'énergie revient à prendre grosso modo
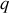protons et les transformer en
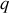neutrons, ainsi
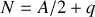et
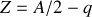, si bien que
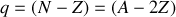. L'énergie due à ce changement peut s'écrire comme
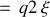avec un espacement
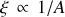entre les niveaux d'énergies peuplés par les protons et neutrons. Ce calcul fournit le terme négatif d'effet d'asymétrie comme :
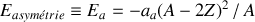
L'énergie de mise en pairs de spins nucléaires
Le dernier terme représente la stabilité particulière associée avec les binômes de spins de protons et neutrons dans les états quantiques du noyau. Les protons comme les neutrons sont des fermions, et deux fermions ne peuvent pas occuper le même état quantique par le principe d'exclusion de Pauli. Protons (et neutrons) minimisent leur énergie en s'appariant (par paires de spins inverses) et les noyaux pairs-pairs sont donc plus stables que les pairs-impairs et que les impairs-impairs. Ce terme est choisi pour être positive,
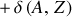, lorsque
et
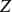sont paires, et négative,
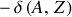, lorsqu'ils sont impaires. Le terme est pris comme nul autrement lorsque
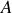est impaire.
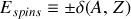
Une expression cumulée s'ensuit de l'addition de ces contributions, elle s'écrit ainsi :
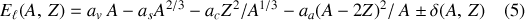
Les coefficients constants de l'équation (4) sont déterminés numériquement en comparant les rendements de l'équation
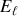pour les noyaux et isotopes (
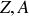), avec des valeurs mesurées. Les valeurs de ces coefficients, mises à jour récemment, sont :
,
,
,
,
.
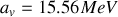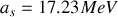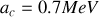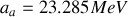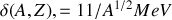L'équation (5) fournit la forme de l'énergie de liaison par nucléon, par division simple par
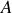, comme suit :
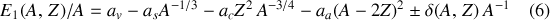
Remarque :
Le proton et le neutron ont un moment angulaire
issu d'un spin nucléaire
qui est à
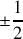pour les deux ; ce moment angulaire est
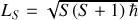. Les moments magnétiques de protons et neutrons, qui sont différents un de l'autres, sont tous les deux donnés en magnéton nucléaire
.
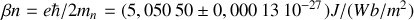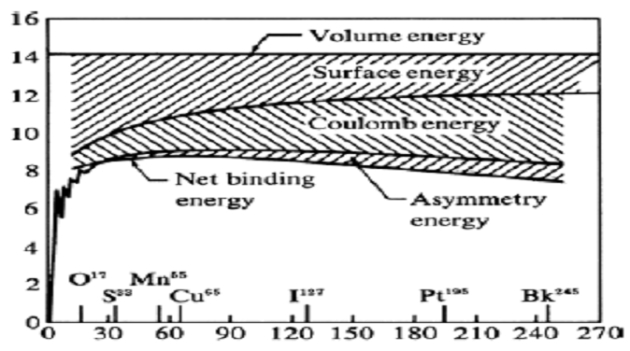
Les contributions relatives de chaque terme de l'équation (6) sont présentées dans la Fig. 22 (sans application de la formule à de trop petits
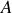). Noter la valeur relativement constante du terme de volume. La correction due au terme de surface du noyau est la plus importante pour les noyaux légers pour lesquels la fraction de nucléons se trouvant à la surface est importante. Comparer cela avec la correction due au terme de l'énergie électrostatique qui est importante pour les noyaux lourds pour lesquels
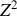devient important. Par ailleurs, l'énergie d'asymétrie est un effet relativement petit sauf pour grand
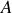, lorsque le rapport
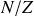devient grand (voir le cours sur la désintégration nucléaire en fonction du temps où l'on explicite l'argumentation de stabilité qui exige un
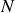croissant par rapport à
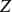pour les noyaux lourds).
