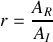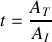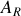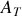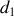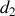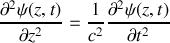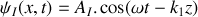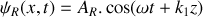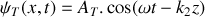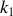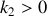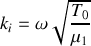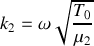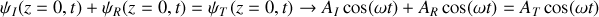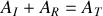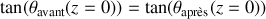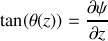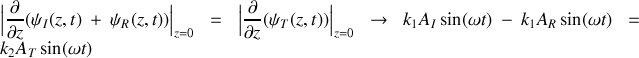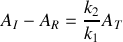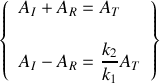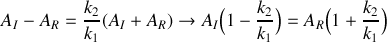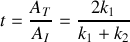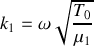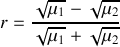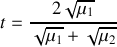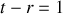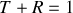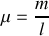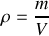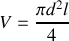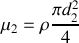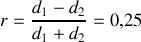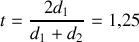Énoncé
Deux cordes de masses linéiques
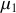 et
et
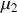 sont attachées en un point de jonction
sont attachées en un point de jonction
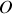 pour former une longue corde tendue horizontalement suivant l'axe
pour former une longue corde tendue horizontalement suivant l'axe
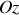 avec une force de tension
avec une force de tension
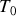 . Le point
. Le point
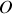 se situe en l'abscisse
se situe en l'abscisse
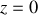 .
.
Une onde transversale progressive se propageant dans le sens des
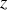 croissants (l'onde incidente) arrive au niveau de la jonction
croissants (l'onde incidente) arrive au niveau de la jonction
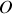 . Il s'agit d'une onde sinusoïdale d'amplitude
. Il s'agit d'une onde sinusoïdale d'amplitude
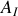 et de la pulsation
et de la pulsation
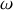 . Elle donne naissance à une onde réfléchie se propageant dans le sens des
. Elle donne naissance à une onde réfléchie se propageant dans le sens des
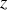 décroissants ainsi qu'à une onde transmise se propageant dans le sens des
décroissants ainsi qu'à une onde transmise se propageant dans le sens des
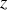 croissants. Ces deux ondes sont aussi sinusoïdales et progressives (voir figure 1).
croissants. Ces deux ondes sont aussi sinusoïdales et progressives (voir figure 1).
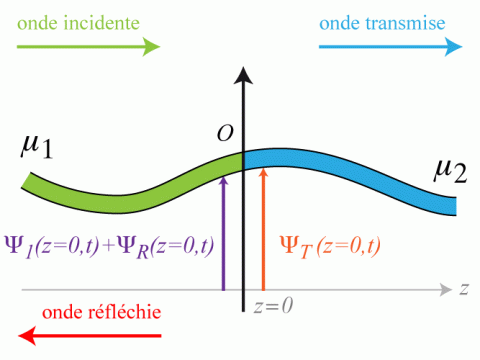
Donner, en notation réelle, les expressions mathématiques des ondes incidentes, réfléchies et transmises. Quelle est la relation de dispersion dans la corde de masse linéique
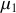 ?
?Quelle est la relation de dispersion dans la corde de masse linéique
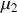 ?
?En s'appuyant sur les conditions de continuité caractérisant le passage de l'onde de la corde 1 vers la corde 2, déduire les deux équations liant les amplitudes des ondes incidentes, transmises et réfléchies.
Donner le coefficient de réflexion
 et de transmission
et de transmission
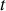 en amplitude en fonction de
en amplitude en fonction de
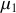 et de
et de
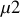 .
.On attache en
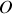 un fil d'acier 1 de diamètre
un fil d'acier 1 de diamètre
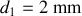 à un fils d'acier 2 de diamètre
à un fils d'acier 2 de diamètre
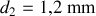 . Calculer, pour l'onde qui se propage du fil 1 vers le fil 2, les coefficients
. Calculer, pour l'onde qui se propage du fil 1 vers le fil 2, les coefficients
 et
et
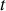 .
.