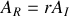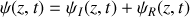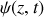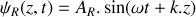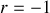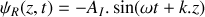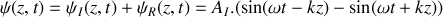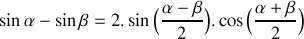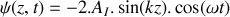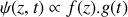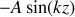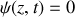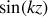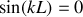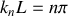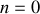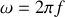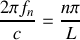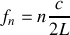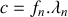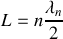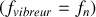Énoncé
Une onde transversale se propage dans une corde de longueur finie
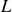 . L'onde est émise et entretenue par un vibreur sinusoïdal situé en
. L'onde est émise et entretenue par un vibreur sinusoïdal situé en
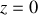 . Le déplacement transversal associé à cette onde incidente à l'abscisse
. Le déplacement transversal associé à cette onde incidente à l'abscisse
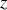 et à l'instant
et à l'instant
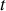 peut s'écrire, en notation réelle, sous la forme
peut s'écrire, en notation réelle, sous la forme
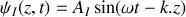 et est solution de l'équation d'onde
et est solution de l'équation d'onde
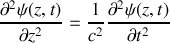 à la condition que
à la condition que
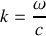 (relation de dispersion pour que
(relation de dispersion pour que
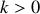 , voir exercice de référence). On considère ici que l'amplitude du vibreur est négligeable si bien que le déplacement transversal est nulle en
, voir exercice de référence). On considère ici que l'amplitude du vibreur est négligeable si bien que le déplacement transversal est nulle en
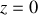 . L'extrémité
. L'extrémité
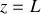 est attachée à un support fixe.
est attachée à un support fixe.
La corde étant fixe, le coefficient de réflexion
 en amplitude à l'abscisse
en amplitude à l'abscisse
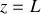 est égal à -1.
est égal à -1.a) En justifiant votre réponse, donner le déplacement transversal
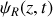 associé à l'onde réfléchie en fonction de
associé à l'onde réfléchie en fonction de
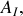
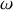 ,
,
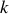 .
.b) En déduire que le déplacement transversal de l'onde résultante qui s'est établie dans la corde s'écrit sous la forme
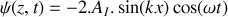 . Justifier le nom d'onde stationnaire et ses conditions de survie.
. Justifier le nom d'onde stationnaire et ses conditions de survie.À partir du résultat de la question 1.b), déterminer les fréquences propres
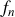 de l'onde stationnaire en fonction d'un entier naturel strictement positif
de l'onde stationnaire en fonction d'un entier naturel strictement positif
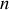 , de la vitesse
, de la vitesse
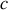 et de la longueur
et de la longueur
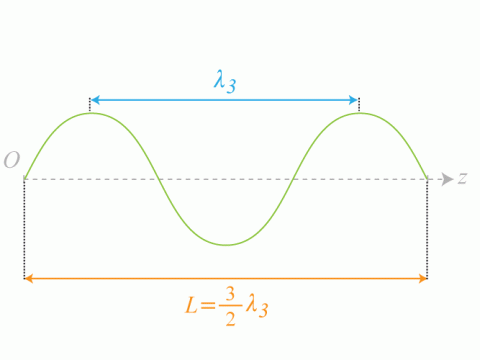
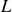 de la corde. En déduire la relation qui lie la longueur
de la corde. En déduire la relation qui lie la longueur
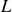 de la corde à la longueur d'onde
de la corde à la longueur d'onde
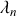 .
.Expliquer le phénomène de résonance et donner sa condition d'existence.
Sans faire de calculs, expliquer quelle est théoriquement l'amplitude du déplacement transversal à la résonance.
Qu'en est-il en réalité ? Si elle est différente, pourquoi ?