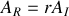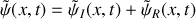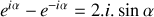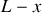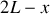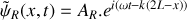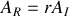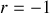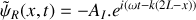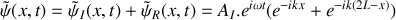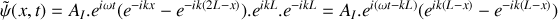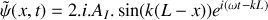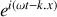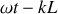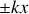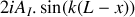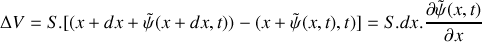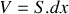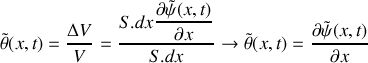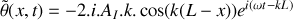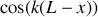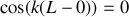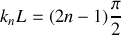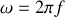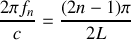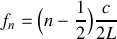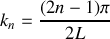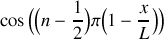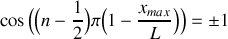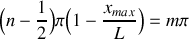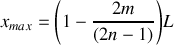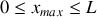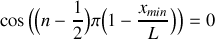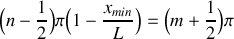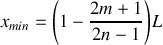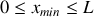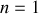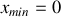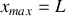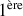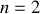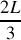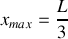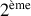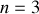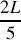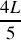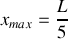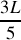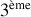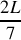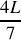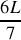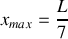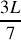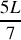Énoncé
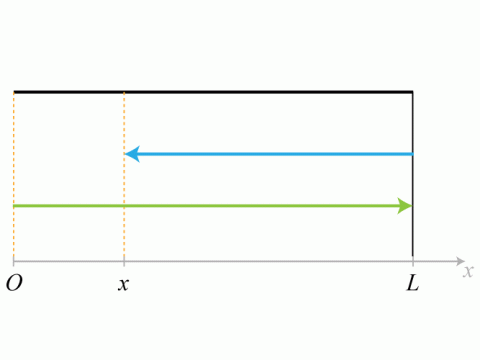
Une onde acoustique se propage dans un tube de longueur finie
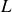. L'onde est émise par un haut-parleur situé en
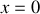. Le déplacement particulaire associé à cette onde incidente à l'abscisse
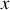et à l'instant
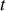s'écrit sous la forme
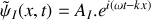et solution de l'équation d'onde
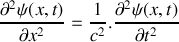à la condition que
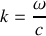(relation de dispersion pour
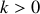). Le tube est semi-fermé tel que l'extrémité
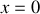est ouverte et l'extrémité
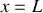est fermée.
Le tube étant fermé, le coefficient de réflexion en amplitude en
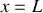pour les déplacements particulaires est égal à -1.a) En justifiant votre réponse, donner en notation complexe le déplacement particulaire
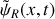associé à l'onde réfléchie en fonction de
,
,
,
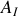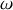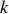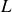.En déduire que le déplacement particulaire de l'onde résultante qui s'est établie dans le tube s'écrit sous la forme
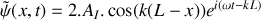. Justifier le nom d'onde stationnaire.La dilatation
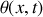d'une tranche de fluide est son accroissement relatif de volume pendant le passage d'une onde acoustique telle que
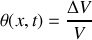. Montrer que l'on peut écrire simplement
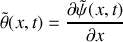et en déduire l'expression de
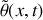.À partir du résultat de la question 1.c), déterminer les fréquences
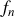, pour lesquelles des résonances de dilatation peuvent apparaître dans le tube, en fonction d'un entier naturel strictement positif n, de la vitesse
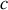et de la longueur
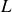du tube.Trouver l'expression de la position des maxima
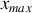et des minima
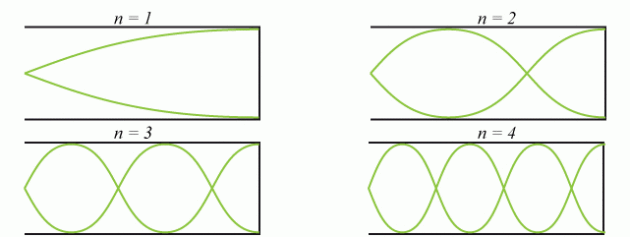
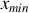de dilatation dans le tube en fonction de L. Représenter graphiquement le comportement de l'onde pour chaque résonance jusqu'à la troisième harmonique (
).
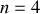