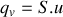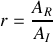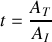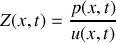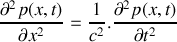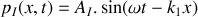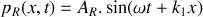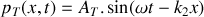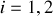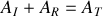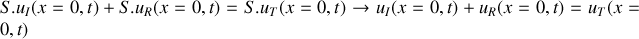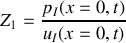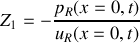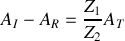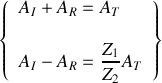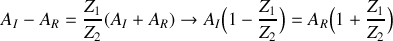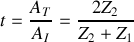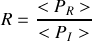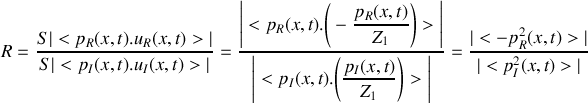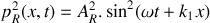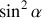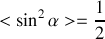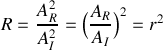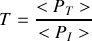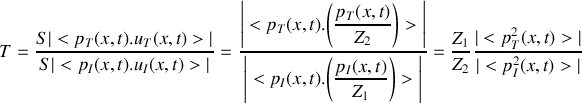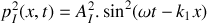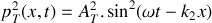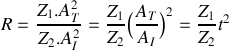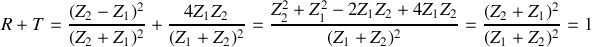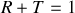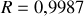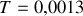Énoncé
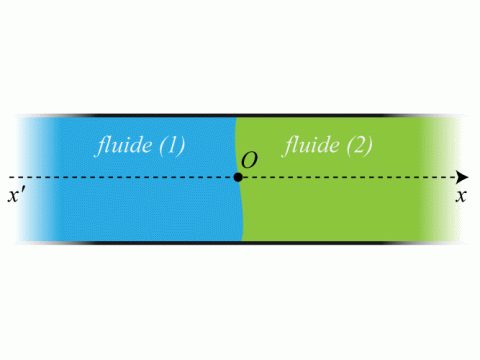
Un tube cylindrique de longueur infinie et de section constante
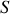 , contient deux fluides (1) et (2) de résistivité acoustique
, contient deux fluides (1) et (2) de résistivité acoustique
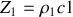 et
et
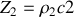 , respectivement. L'origine
, respectivement. L'origine
 du repère est placé à l'abscisse
du repère est placé à l'abscisse
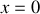 de sorte que le fluide (1) soit dans la région des
de sorte que le fluide (1) soit dans la région des
 et le fluide (2) dans la région des
et le fluide (2) dans la région des
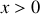 (voir figure 1).
(voir figure 1).
Une onde acoustique plane progressive se propageant dans le sens des
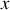 croissants (l'onde incidente) arrive au niveau de la jonction en
croissants (l'onde incidente) arrive au niveau de la jonction en
 . Cette onde s'accompagne d'une surpression acoustique s'écrivant sous la forme
. Cette onde s'accompagne d'une surpression acoustique s'écrivant sous la forme
 et étant solution de l'équation d'onde
et étant solution de l'équation d'onde
 avec
avec
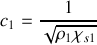 , à la condition que
, à la condition que
 (relation de dispersion pour
(relation de dispersion pour
 ). Elle donne naissance à une onde réfléchie se propageant dans le sens des
). Elle donne naissance à une onde réfléchie se propageant dans le sens des
 décroissants ainsi qu'à une onde transmise se propageant dans le sens des
décroissants ainsi qu'à une onde transmise se propageant dans le sens des
 croissants. Ces deux ondes sont aussi sinusoïdales et progressives.
croissants. Ces deux ondes sont aussi sinusoïdales et progressives.
Donner, en justifiant votre réponse, les expressions mathématiques réelles des surpressions acoustiques associées aux ondes réfléchies et transmises.
La résistivité acoustique d'un fluide à l'abscisse
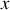 et à l'instant
et à l'instant
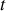 s'écrit :
s'écrit :
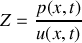 .
.a) En s'appuyant sur les conditions de continuité caractérisant le passage de l'onde du fluide (1) vers le fluide (2), déduire les deux équations liant les amplitudes des ondes incidentes, transmises et réfléchies.
b) Donner le coefficient de réflexion
 et de transmission
et de transmission
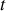 en amplitude en fonction de
en amplitude en fonction de
 et de
et de
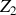 .
.La puissance sonore moyenne véhiculée par chaque onde acoustique est donnée par la relation
 .
.a) Déterminer le coefficient de réflexion
 et de transmission
et de transmission
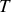 relatif aux puissances acoustiques. Quelle remarque peut-on faire au sujet de ces coefficients?
relatif aux puissances acoustiques. Quelle remarque peut-on faire au sujet de ces coefficients?b) Calculer
 et
et
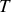 si le milieu (1) est de l'air (
si le milieu (1) est de l'air (
 ) et le milieu (2) est de l'eau (
) et le milieu (2) est de l'eau (
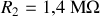 ).
).