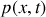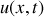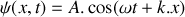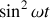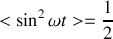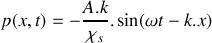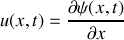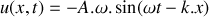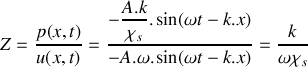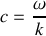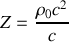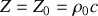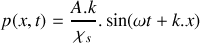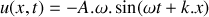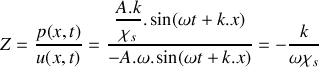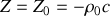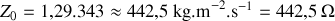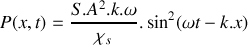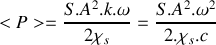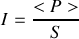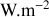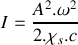Énoncé
Un tuyau cylindrique de longueur infinie et de section constante
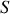 , contient un fluide qui au repos est à la pression
, contient un fluide qui au repos est à la pression
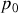 , à la température
, à la température
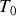 et à une masse volumique
et à une masse volumique
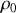 .
.
Le passage d'une onde acoustique plane progressive s'accompagne d'un déplacement particulaire des molécules noté
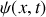 . On notera également la vitesse de déplacement
. On notera également la vitesse de déplacement
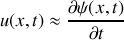 et la surpression acoustique liée au passage de l'onde
et la surpression acoustique liée au passage de l'onde
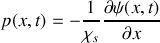 où
où
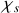 est le coefficient de compressibilité isentropique du fluide.
est le coefficient de compressibilité isentropique du fluide.
L'onde acoustique se déplaçant dans le sens des
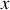 croissants, le déplacement particulaire peut s'écrire sous la forme
croissants, le déplacement particulaire peut s'écrire sous la forme
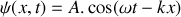 et est solution de l'équation d'onde
et est solution de l'équation d'onde
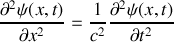 avec
avec
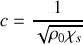 , à la condition que
, à la condition que
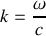 (relation de dispersion pour que
(relation de dispersion pour que
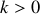 , voir exercice de référence).
, voir exercice de référence).
On se limitera aux mouvements de faibles amplitudes et on négligera l'action de la pesanteur ainsi que toute viscosité ou frottements.
On appelle résistivité acoustique (ou impédance) du milieu de propagation la grandeur caractéristique définie par :
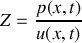 .
.a) montrer que
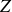 est une constante
est une constante
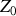 qu'on exprimera en fonction de
qu'on exprimera en fonction de
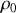 et c.
et c.b) Que devient ce résultat si l'onde se propage dans le sens des
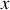 décroissants?
décroissants?c) Calculer la résistivité acoustique
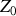 dans l'air avec
dans l'air avec
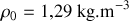 et
et
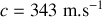 . L'exprimer dans en unité S.I. et M.K.S.A.
. L'exprimer dans en unité S.I. et M.K.S.A.La puissance sonore instantanée
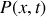 véhiculée par cette onde acoustique est donnée par la relation
véhiculée par cette onde acoustique est donnée par la relation
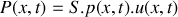 .
.a) Exprimer la puissance sonore temporelle moyenne
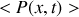 en fonction de
en fonction de
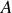 ,
,
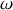 , c,
, c,
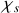 , S pour une onde se propageant dans le sens des
, S pour une onde se propageant dans le sens des
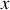 croissants.
croissants.b) En déduire l'intensité sonore
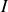 d'une onde se propageant dans le sens des
d'une onde se propageant dans le sens des
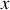 croissants.
croissants.