Quelques propriétés des moments d'inertie
Deux extensions des moments d'inertie peuvent être pointées : le moment d'inertie par rapport à un point ainsi que celui par rapport à un plan.
Ils sont obtenus par une généralisation dimensionnelle de la somme des produits des masses par les distances au carré, au point ou au plan respectivement.
Le moment d'inertie par rapport à l'origine des axes,
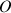par exemple, est tel que :
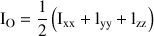,une relation obtenue directement en faisant la somme des
moments axiaux.
Les grandeurs
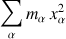ou
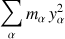ne sont rien d'autres que des moments d'inertie par rapport à des plans, respectivement
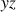et
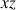; ils mettent en jeu la distance de chaque particule aux plans concernés.
