Rotation libre d'une toupie symétrique
Le cas général de la rotation libre d'une toupie symétrique est considéré. (Fig. 6)
Le traitement est ici relativement intuitif et le poids de la toupie est négligé.
Il deviendra de plus en plus "démontré" et mathématique au fil des chapitres et de l'élaboration du formalisme décrivant le solide.
Syntaxe : Quels axes pour quelles rotations ?
Le centre de masse de la toupie est identifié et noté
.
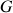S'agissant de rotations, tous les moments d'inertie sont évalués par rapport au CDM..
La toupie symétrique présente
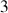axes de symétrie, et directions principales, dont deux sont équivalents.
Sa rotation naturelle s'effectue autour du 3ème axe, passant par sa pointe (direction
).
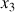La vitesse angulaire associée à cet axe est notée
.
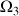Les deux autres directions principales (
,
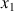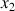) sont dans le plan perpendiculaire à l'axe
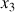passant par le CDM
.
L'égalité entre les deux moments d'inertie de la toupie,
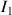et
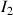, indique que les deux directions
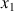et
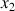sont équivalentes du point de vue des rotations.
Une seule rotation (selon
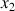selon la Fig. 6) est utile pour la description des rotations de la toupie : la démonstration sera effectuée dans l'application des rotations d'Euler et du calcul de l'énergie cinétique.
Ainsi ces
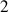rotations angulaires,
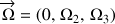peuvent être prises en compte sans perte de généralité : le vecteur vitesse angulaire dans le plan (
).
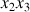Sur la Fig. 6, le plan de la figure représente le plan 'vertical' x_2x_3 ; l'axe x_1 lui est perpendiculaire et rentrant.
Ainsi lorsque la toupie tourne autour de l'axe x_3 dans le sens trigonométrique (opposé au mouvement des aiguilles d'une montre), elle décrit également un cône de précession dans le sens trigonométrique dont la justification suit.
La rotation libre est produite par la conservation du moment cinétique.
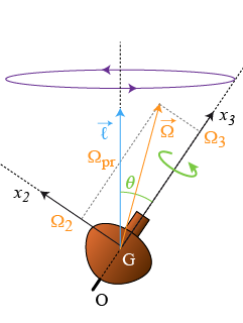
Sur la Fig. 6 la direction du moment cinétique, constante, est choisie confondue avec celle de la verticale.
Ceci représente un cas général : il produit une inclinaison de la vitesse angulaire totale par rapport au moment cinétique.
Le moment cinétique total qui résulte des rotations de la toupie s'écrit selon la composition vectorielle suivante :
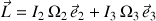
Sa conservation implique qu'il reste dans le plan (
,
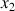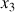) selon une direction fixe : l'axe
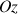vertical.
Dans ce qui suit, deux éléments sont incontournables :
la constance vectorielle du moment cinétique
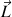et l'inclinaison de l'axe de rotation principal de la toupie (et de la rotation propre
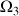) par rapport à la verticale ce qui incline la rotation totale
.
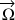Le vecteur-vitesse rotation totale et les composantes sont représentées sur la Fig. 6.
Ainsi la projection de
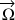sur l'axe
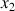coupe l'axe vertical (et axe du moment cinétique) : ceci donne lieu à une vitesse angulaire portée par l'axe vertical dont la signification apparaît dans ce qui suit.
Démonstration : Existence de la précession par analyse géométrique
Cette analyse se focalise sur les points de l'axe
.
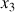Tous ces points sont chacun soumis à une vitesse linéaire
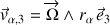issue de la rotation totale et fonction de leur position sur l'axe, par rapport à l'origine fixe
.
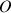Chacune de ces vitesses est perpendiculaire au plan (
,
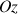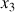), est parallèle à la direction de
.
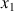Ces vitesses produisent une rotation de l'axe
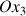de la toupie autour de l'axe du moment cinétique et donc une rotation du plan (
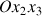) autour de l'axe fixe
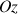: ce mouvement d'ensemble du solide est la précession régulière qui s'ajoute à la rotation propre autour de l'axe
.
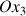Pour déterminer la vitesse de précession, il suffit d'écrire la conservation du moment cinétique et de noter ses projections.
Avec la notation suivante :
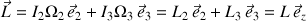
L'inclinaison de l'axe de la toupie par rapport à la verticale étant notée
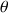, les deux composantes du moment cinétique sur les axes de la toupie sont :
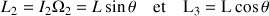
Par projection, la vitesse angulaire de précession est :
.
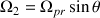Elle s'écrit également
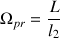en fonction des paramètres du problème.
Remarque :
Cette démonstration ne met en jeu aucune force et s'appuie sur l'inclinaison qui existe entre directions du moment cinétique et vitesse angulaire totale.
Elle est intuitive et constitue une bonne entrée en matière pour décrire le phénomène de précession.
Deux démonstrations seront proposées en application des rotations d'Euler et des équations d'Euler.
