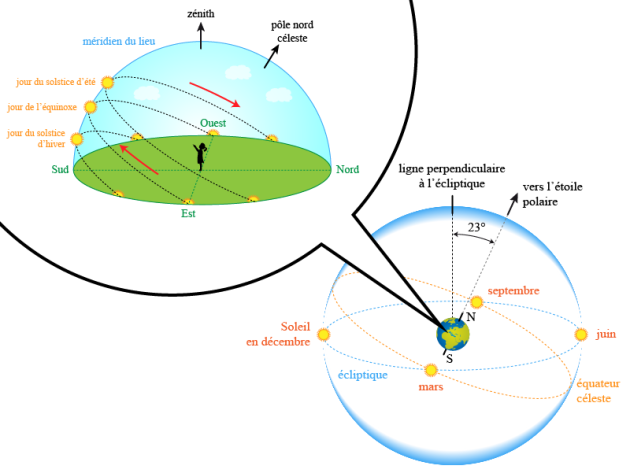
Le phénomène de précession
Ce phénomène est présent dans la nature et présenté par des solides indéformables (toupies par exemple) mais également par ceux déformables (précession des équinoxes).
Selon le schéma qui précède, la rotation autour d'un axe du solide, distinct de celui du vecteur moment cinétique (constant), entraîne la précession de l'ensemble du solide autour de l'axe du moment cinétique.
La vitesse de précession dépend du moment angulaire initial et elle est constante.
Dans le cas des mouvements de planètes, considérées comme des solides indéformables, l'existence d'un moment cinétique constant peut provenir de rotations initiales lors de la formation des planètes du système solaire.
Ainsi le mouvement plan propre aux forces centrales produit le plan de l'écliptique commun à l'ensemble des 8 planètes tournant autour de l'attracteur qu'est le soleil : ceci indique l'existence, pour chacune, d'un moment cinétique orbital perpendiculaire au plan de l'écliptique.
De surcroît, les axes propres de rotation sont inclinés par rapport au plan de l'écliptique (\,80° pour la Terre, quelques degrés pour Uranus) : les conditions sont réunies pour produire une précession de leurs axes de rotation propre.
Mais les planètes, dont la Terre, sont des solides déformables par le mouvement des eaux et gaz qui les constituent.
Ainsi un second schéma permet d'expliquer la précession.
il s'agit de l'existence d'un couple de forces.
En effet ces deux forces, de même direction et intensité, de sens opposés et de points d'application différents produisent une rotation dont le moment cinétique est constant ou faiblement variable au cours du temps à l'échelle des autres phénomènes mis en jeu.
À l'équinoxe, où le soleil est exactement au zénith sur l'équateur terrestre, deux fois l'an, le jour et la nuit ont une durée égale. Le plan de l'écliptique croise alors celui de l'équateur céleste, perpendiculaire à l'axe propre de rotation de la Terre.
Entre deux mêmes équinoxes, il s'est écoulé une année tropique de 365j 5h 48min, alors que par rapport aux étoiles, le passage de la Terre au même endroit dans la même direction s'effectue en 365j 6h 9min : c'est l'année sidérale. (Fig. 7)
Cette différence trouve son origine dans la précession des équinoxes laquelle décrit la rotation de l'axe de la Terre autour d'un axe perpendiculaire au plan de l'écliptique en formant ainsi un cône en 26 000 années environ.
Ce déplacement angulaire de l'axe de la Terre a été évalué à moins de 1° d'angle par siècle par Hipparque de Nicée en 130 avant JC.
Hipparque disposait d'observations suffisamment précises sur la position du Soleil par rapport aux étoiles, mesures effectuées sur 169 années, et qu'il a comparé avec ses propres mesures réalisées sur les éclipses de la Lune et du Soleil.
Cette valeur a été corrigée à 50,290966'' par an soit 1° tous les 72 ans.
La précession des équinoxes est associée au couple qu'exercent les forces de marées de la Lune et du Soleil sur le renflement équatorial de la Terre et qui déplacent un excès de masse équatoriale autour du plan de l'écliptique.
Ce phénomène explique notamment
du retard du cycle des saisons (année tropique) d'environ 20min par rapport au mouvement de la Terre par rapport aux étoiles (année sidérale) entraînant
les règles relatives aux années bissextiles.
Dans le cas de la toupie symétrique, solide indéformable, la précession ne peut être interprétée en termes de couple de forces même si la toupie est soumise d'une part à son poids, vertical, et d'autre part à la réaction du support au niveau de la pointe, également selon la verticale, deux forces égales, de même direction et de sens opposés pouvant constituer un couple.
Un moment cinétique constant implique une inclinaison constante de la toupie et le mouvement de précession décrit ci-avant.
Si le poids de la toupie agit sur son mouvement alors son effet concernera directement l'angle
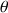et un mouvement additif à la précession sera décrit : la nutation.
(Voir le chapitre sur les angles d'Euler et ses applications)
Exemple : Précessions
Ainsi le phénomène de précession a été analysé depuis l'antiquité par ceux qui scrutaient le mouvement des planètes et étoiles dont notre soleil,... vu de la Terre.
L'exemple de la toupie symétrique met en évidence le rôle de la direction de la vitesse angulaire, différente de celle fixe du moment cinétique, ou de la pesanteur, ou d'un autre champ extérieur.
1) Précession autour d'une direction fixe
La précession a lieu autour de la direction fixe, jusqu'ici l'axe vertical
.
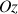Si matériellement l'axe qui effectue la précession est l'axe propre
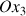de la toupie, la grandeur physique qui lui correspond est
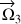ou encore
.
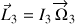Aux dimensions près, le mouvement de précession autour de la direction d'un vecteur
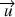(un vecteur qui peut être le moment cinétique total
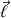notamment) est décrit par l'équation du mouvement suivante :
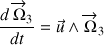
La dimension du vecteur
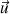est celle d'une vitesse angulaire (
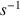) : il s'agit de la vitesse angulaire de précession notée
.
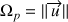Il reste à vérifier que cette vitesse de précession est vectoriellement constante, assurant au passage une inclinaison constante.
Ce qui est vérifié de fait par construction puisque
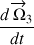) est perpendiculaire à
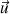et
.
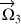Ses composantes sur ces deux vecteurs sont nulles. Ceci implique que
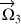a une composante constante sur
.
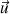Au cours du temps,
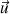est un vecteur constant.
Les rotations de vecteurs dans un produit mixte peuvent également être utilisées.
De la même façon, la projection sur
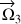est un vecteur constant et sa norme est constante.
Cette forme de dérivée exprime bien la rotation de
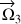autour de la direction fixe représenté par le vecteur
.
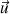Cette rotation de l'axe
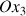produit la rotation de tout le solide et donc de l'axe portant
.
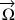La vitesse angulaire de la précession est la projection de
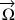sur l'axe fixe (démonstration ci-dessus pour la toupie).
2) Si couple de forces il y a ...
Lorsqu'un couple de forces, de moment
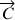, est à l'origine de la précession d'un axe de rotation, elle produit une variation temporelle du moment cinétique telle que
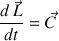(théorème du moment cinétique , chapitre II).
La vitesse angulaire de précession est telle que :
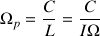
Plus généralement, la précession d'un axe de rotation implique la précession du moment angulaire qui lui correspond.
Cette précession de moment angulaire se produit également en présence de champ extérieur fixe.
Outre la toupie ou le gyroscope qui possède un mouvement de précession, et de nutation si le moment résultant n'est pas nul (voir les équations d'Euler), d'autres systèmes physiques présentent ce phénomène, toujours selon les schémas développés ci-dessus.
A titre d'exemples, les différents moments suivants, et rotations propres suivantes, associés à des champs vectoriels fixes provoquent le phénomène de précession.
Le plan d'oscillation du pendule de Foucault subit une précession due à la rotation de la Terre sur son axe, induite par la force d'inertie de Coriolis.
Plus généralement, tout moment cinétique propre ou orbital peut subir une précession sous l'influence (champ) d'autres corps célestes (précession du périhélie, par exemple).
À l'échelle atomique, une particule plongée dans un champ magnétique voit son moment magnétique propre effectuer une précession autour du champ extérieur : c'est la précession de Larmor.
La précession de Thomas est un mouvement décrit par le moment cinétique propre de spin d'une particule lorsqu'elle est accélérée.
Lorsqu'elle est plongée dans un champ gravitationnel, la précession du spin s'appelle l'effet Sitter.
