Les forces internes de cohésion sont des forces surfaciques appelées contraintes internes. Pour les appréhender, découpons un système en deux parties et , étant le sous-système sur lequel on cherche à déterminer l'action de cohésion due au sous-système . Comme le montre la figure 3, on peut ainsi définir le vecteur contrainte agissant sur une facette autour du point M :

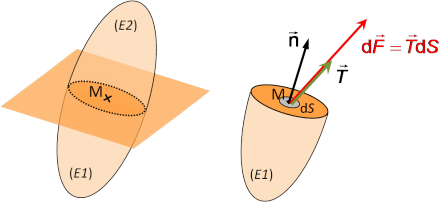
Le torseur des efforts de cohésion sur la facette de surface S se réduit en un point A à :

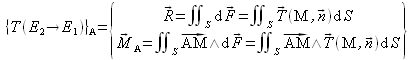
Ainsi, dans le repère lié à la facette (figure 4), le vecteur contrainte peut s'écrire en fonction d'une composante normale et d'une composante tangentielle :

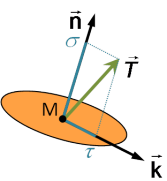
Dans ce contexte, on parle pour de tension (plus précisément de traction si la composante est positive, ou de compression si elle est négative), et pour de cisaillement.