Puisque le tenseur des contraintes est symétrique, ses valeurs propres sont réelles et les directions propres associées (vecteurs propres) sont orthogonaux deux à deux. On notera donc 
, 
, et 
les trois valeurs propres en les appelant contraintes principales. Les trois vecteurs propres associés, notés 
, 
et 
, définissent donc un repère orthonormé appelé repère principal.
Attention :
Par convention, on ordonnera toujours les contraintes principales de sorte que 
.
Il en résulte que dans le repère principal le tenseur des contraintes est diagonal, et qu'une contrainte s'exerçant sur une facette de normale 
s'explicite :
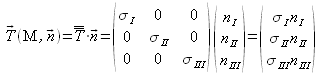
où 
sont les composante de 
dans le repère principal.
