Compte tenu du théorème de Cauchy, la contrainte 
s'explicite à l'aide des 9 éléments 
qui composent le tenseur des contraintes noté 
. On peut donc formuler la contrainte s'exerçant sur une facette de normale 
comme :
ou bien plus explicitement comme :
Remarque :
D'un point de vue pratique, chacun des éléments 
du tenseur des contraintes rend compte d'une contribution clairement identifiable : le premier indice i est l'indice de projection (direction selon laquelle s'exerce la contribution) ; le second indice j repère l'orientation de la surface sur laquelle s'exerce la contribution. A titre d'exemple 
correspond à la composante suivant 
de la contrainte qui s'exerce sur la facette de normale 
.
Exemple :
A partir de la connaissance du tenseur des contraintes au point M, on peut déterminer les 3 composantes de la contrainte qui s'exerce sur la facette de normale 
(figure 7) :
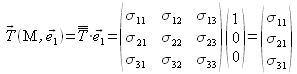
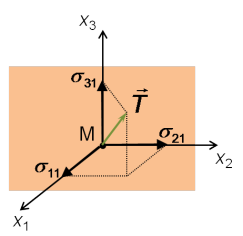
Compte tenu du principe de l'action et de la réaction, on obtiendrait la contrainte opposée en considérant la facette orientée selon 
.
Attention :
En exploitant la condition d'équilibre (démonstration du théorème de Cauchy) appliquée au moment résultant, il est possible de démontrer que le tenseur des contraintes est nécessairement symétrique. On tiendra donc pour acquis que 
.
