En choisissant une facette de normale au point M, la contrainte qui y est exercée définit nécessairement une direction perpendiculaire à et contenue dans le plan de la facette : il s'agit de la direction portée par le vecteur unitaire (figure 8).

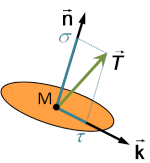
On peut ainsi projeter la contrainte sur les deux directions et :

où et sont respectivement désignées comme les composantes normale et tangentielle de la contrainte.

Afin d'étudier et caractériser la contrainte en M en fonction des différentes orientations possibles de la facette, une méthode graphique consiste à représenter les valeurs de et lorsque varie : il s'agit du diagramme de Mohr.

Dans ce contexte, il est possible de formuler les relations suivantes entre ces deux composantes :

On peut alors, dans le repère lié à la facette , représenter le lieu des points P tels que lorsque varie. Pour ce faire, il faut établir le lien entre le repère lié à la facette et le repère principal ; on obtient alors facilement le système linéaire de 3 équations à 3 inconnues suivant :

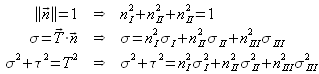
Pour et fixées, les solutions possibles concernant l'orientation de sont donc :

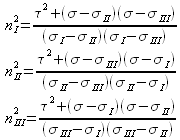
où, respectant la convention, les contraintes principales vérifient .

Pour chacune de ces trois relations, le terme de gauche est nécessairement positif et impose que numérateur et dénominateur à droite doivent être de même signe. Il en résulte que :

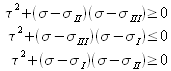
Les trois inégalités obtenues définissent alors, dans le repère , des surfaces délimitées par des demi-cercles, comme le montre la figure 9.

Figure 9

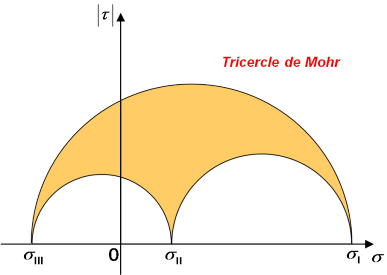
Cette représentation, appelée tri-cercle de Mohr, permet d'appréhender que tous les états de contrainte ne sont pas permis : seuls ceux correspondant à la surface colorée sont physiquement possibles.