Il s'agit ici de simplifier l'étude d'un état de contrainte en se plaçant dans une configuration où la contrainte s'exerce nécessairement dans un plan. Pour envisager une telle configuration, deux situations sont envisageables.
Prenons par exemple 
. Dans le repère principal, on a donc :
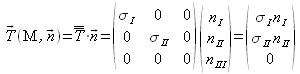
ce qui signifie que quelle que soit 
, la contrainte s'exerçant est nécessairement contenue dans le plan 
. Il s'agit donc bien d'un état plan de contrainte.
Choisissons par exemple les facettes dont l'orientation 
reste perpendiculaire à l'axe 
; on a donc 
, et il en résulte que :
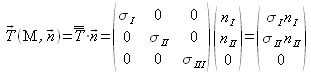
conduisant à une contrainte nécessairement contenue dans le plan 
. Il s'agit donc du même état plan de contrainte que celui décrit pour la situation (a).
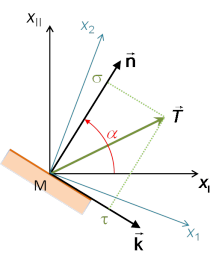
Dans les deux cas, on considère alors une situation dans laquelle la contrainte s'exerce dans un même plan, celui perpendiculaire à 
. Par ailleurs, pour simplifier le raisonnement, on pourra choisir un repère orthonormé 
de telle sorte que 
, ce qui implique que 
et 
décrivent le même plan, celui dans lequel s'exerce la contrainte (figure 10).
Reprenons la démarche suivie pour aboutir au tri-cercle de Mohr. Puisque 
, l'équation :
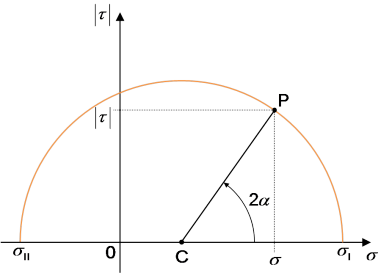
permet d'annuler le numérateur et conduit à l'équation 
, qui est celle d'un cercle : le cercle de Mohr. D'un point de vue pratique, cela signifie que les états de contraintes plans possibles correspondent aux valeurs de 
et 
décrivant un demi-cercle dans le diagramme de Mohr 
, de telle sorte que 
où P est nécessairement un point sur ce demi-cercle (figure 11).
Afin de caractériser et d'exploiter ce cercle, déterminons son équation paramétrique en repérant l'orientation de la normale 
grâce à l'angle 
qu'elle forme avec la direction 
(figure 10). Dans le repère principal, les composantes de la normale se formulent alors : 
et 
. Il vient donc que la composante normale de la contrainte s'écrit en fonction de 
comme :
Et en faisant appel aux relations trigonométriques bien connues 
et 
, on obtient la formulation suivante :
Explicitons alors l'expression de la composante tangentielle de la contrainte en partant de la relation : 
. On trouve :
et en développant :
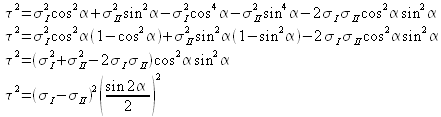
En valeur absolue, la composante tangentielle s'exprime donc :
L'angle 
variant de 0 à 
, les expressions de 
et 
permettent donc de tracer dans le repère 
un demi-cercle de rayon 
et dont le centre C se trouve sur l'axe des abscisses à 
(figure 11).
Remarque :
On peut tracer le cercle entier en permettant au cisaillement 
de prendre des valeurs négatives. Il convient alors de se donner une convention pour orienter la direction 
dans le plan de la facette. On choisira donc de compter positivement le cisaillement lorsqu'il a pour effet de faire tourner la facette dans le sens horaire (le schéma de la figure 10 adopte cette convention).
L'intérêt du cercle de Mohr réside essentiellement dans le fait qu'il permet la détermination de tout état de contrainte plan dès lors que les contraintes principales sont connues. En effet, 
et 
donnent accès au centre et au rayon du cercle et permettent de le tracer. L'orientation de la facette étant définie par sa normale 
, et donc par l'angle 
qu'elle forme avec la direction 
, le point P situé à 
sur le cercle de Mohr permet d'en déduire les composantes normale 
et tangentielle 
de la contrainte subie.
Remarque :
L'étude du cercle de Mohr nous confirme que le cisaillement ne peut excéder, en valeur absolue, le rayon du cercle : 
; et que ce maximum est atteint pour une facette orientée selon la bissectrice des directions principales : 
.
On notera par ailleurs que le cisaillement est nécessairement nul selon les directions principales : pour 
et pour 
.
