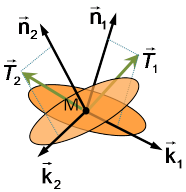
Puisque en un point M il existe une infinité de facettes d'orientation 
différentes (figure 5), le théorème de Cauchy permet de définir l'état de contrainte sur une facette d'orientation quelconque à partir de la connaissance de l'état de contrainte selon trois directions différentes. L'énoncé du théorème est le suivant :
Les composantes du vecteur contrainte en un point M sur une facette de normale
Cet énoncé conduit naturellement à formuler la contrainte s'exerçant sur une facette d'orientation quelconque comme :
Complément :
Démonstration du théorème de Cauchy
Considérons un repère orthonormé dont les vecteurs unitaires sont 
. En un point M du solide, les trois facettes ayant comme normale ces trois vecteurs unitaires subissent les contraintes respectives : 
. Montrons alors que pour 
quelconque, il est possible d'exprimer 
en fonction de 
.
Dans le repère 
, les composantes de 
et de 
peuvent s'expliciter :
On raisonne alors à partir d'un tétraèdre de sommet M, dont 3 des 4 faces sont normales au repère, la quatrième étant orientée selon 
(figure 6).
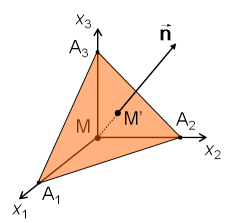
Le tétraèdre étant supposé à l'équilibre la résultante des forces qui agissent dessus doit être nulle. Il en résulte :
d'où :
Établissons alors le lien entre 
et 
, 
, 
, en remarquant que d'une part :
et d'autre part :
Par identification, on en déduit que : 
, 
, et 
; ce qui permet de reformuler la contrainte en M' comme :
soit encore :
Pour obtenir une équation locale, faisons tendre M' vers M en remarquant que dans ces conditions le rapport 
tend vers 0 :
ce qui correspond bien à la formulation du théorème de Cauchy.
Dans ce même repère orthonormé, chacune des trois contraintes de base présente trois composantes ; on a donc :
et la contrainte en M sur la facette de normale 
s'écrit alors :
Les coefficients linéaires 
apparaissent donc comme les éléments d'un tenseur de rang 2 : il s'agit du tenseur des contraintes.
