Rappelons que la force de Lorentz qui s'exerce sur une particule de charge 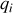plongée dans un champ électrique 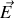et magnétique 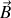dépendant de la coordonnée spatiale 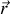vaut

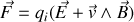
où 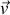représente la vitesse de la particule dans le référentiel du laboratoire.

Par conséquent, le travail 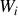nécessaire pour amener la charge d'un point 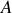à un point 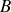le long d'un contour 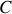vaut l'opposé du travail reçu par la charge, et donc

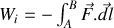
comme 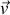est toujours parallèle à 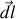le produit vectoriel lui est orthogonal, et la composante magnétique de la force de Lorentz ne travaille pas.

Finalement si nous considérons que 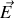dérive d'un potentiel selon 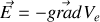le travail devient

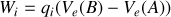
il ne dépend donc pas du chemin suivi.

La convention veut que l'énergie d'une distribution de charges soit égale au travail nécessaire à sa constitution, et souvent on prend de plus un potentiel nul à l'infini ; ainsi si 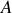est situé à l'infini

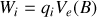
et si nous supposons que le point 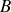est situé en 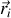et que le potentiel est créé par la loi de Coulomb par un ensemble de 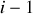charges 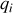situées chacune en

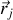
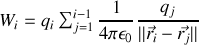
et l'énergie totale d'un ensemble de 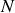charges vaut

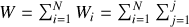
ou encore

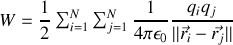
en omettant l'interaction d'une charge avec elle-même dans la somme.

Si comme dans les premiers chapitres nous passons à une distribution de charges continue dans tout l'espace 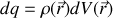il vient

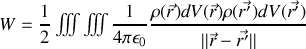
ou encore avec le potentiel électrique

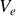
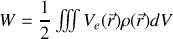
or en électrostatique l'équation de Poisson est toujours vérifiée donc

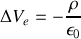
et en substituant 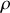il vient

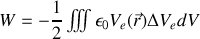
Si nous revenons à 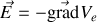en employant une intégration par parties pour chaque coordonnée cartésienne et en remarquant que le terme tout intégré est nul puisque le champ est supposé nul à l'infini il reste

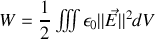
expression que nous privilégierons par la suite.