Nous allons désormais appliquer le même raisonnement que dans le paragraphe précédent au calcul de l'énergie d'une distribution de courants. Encore une fois, l'énergie de la distribution est prise égale au travail d'établissement, égal à l'opposé du travail 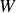reçu par le circuit. Considérons un circuit isolé constitué d'un fil parcouru par un courant 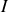homogène en régime permanent.

On a

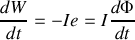
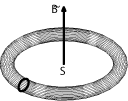
en vertu de la loi de Lenz-Faraday, pour un circuit de surface 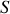subissant un champ magnétique 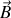de flux 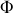à travers cette surface. Notons que ce champ magnétique est créé par le courant 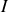lui-même.

Nous en déduisons facilement que

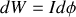
or par définition

Figure 4 : Circuit modèle employé pour le calcul de l'énergie magnétostatique

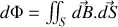
d'autre part si nous considérons que le fil a une section 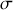d'élément de surface 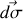l'intensité vaut

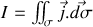
avec 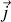la densité de courant.

Finalement

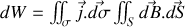
Si nous employons le potentiel vecteur tel que 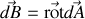une application de la formule de Stokes pour faire disparaître le rotationnel donne

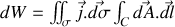
avec 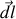élément de longueur du circuit de contour .

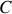En regroupant les intégrales nous voyons apparaître une intégrale sur le volume du fil, et en intégrant à partir d'un temps où l'énergie est nulle (au début de l'établissement supposé très lent de la distribution de courant)

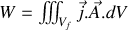
formule élégante, similaire à celle obtenue en électrostatique, et que nous généraliserons à une distribution arbitraire de courants dans tout l'espace en sommant leurs contributions locales par le même raisonnement, et en introduisant comme dans le paragraphe précédent sur l'électrostatique un facteur 1/2 pour éviter le double comptage des interactions mutuelles entre courants.

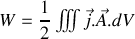
Cependant, en magnéto-statique la forme locale du théorème d'Ampère (sans courant de déplacement) vaut

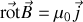
donc l'équation précédente se transforme en

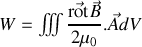
et en intégrant par parties sur chacune des composantes cartésiennes, en se souvenant que 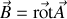et en prenant le champ nul à l'infini ce qui fait disparaître le terme tout intégré il vient

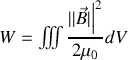
équation que nous retiendrons pour la suite.