Considérons désormais le cas général d'un champ électromagnétique obéissant aux équations de Maxwell, sans supposer une quelconque stationnarité. La force qui s'exerce sur une charge élémentaire 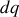animée d'une vitesse 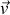par rapport au référentiel du laboratoire est la force de Lorentz qui vaut

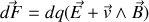
La puissance 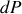de cette force vaut quant à elle

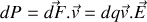
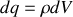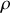puisque la composante magnétique est toujours orthogonale à la trajectoire. Si nous intégrons sur l'espace, avec et la densité de charges il vient pour la puissance totale 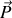déposée sur les charges contenues dans un volume 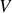par le champ

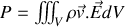
soit encore par définition de la densité de courant

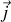
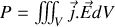
Cette formule est particulièrement utile pour étudier par exemple la puissance obtenue par le chauffage par induction en supposant la forme locale de la loi d'Ohm et en employant le champ de Neumann.

Nous pouvons de plus, à l'inverse du paragraphe précédent, employer l'équation de Maxwell-Ampère avec le courant de déplacement pour remplacer 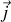dans cette équation ; ainsi

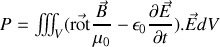
En employant la formule d'analyse vectorielle

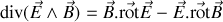
il vient par substitution

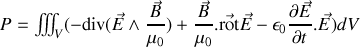
En employant l'équation de Maxwell-Faraday

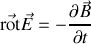
il apparaît

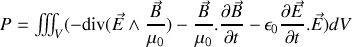
Si nous introduisons la densité totale d'énergie électromagnétique u somme des contributions électrostatiques et magnéto-statiques vues dans les paragraphes précédents

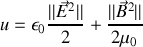
ainsi que le vecteur 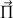dit de Poynting tel que

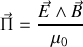
nous remarquons dans l'expression de 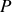après application de la formule de Green- Ostrogradski pour transformer le premier terme en intégrale de surface sur la surface 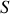du volum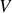e que

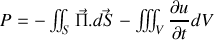
ce qui signifie que la puissance électromagnétique déposée dans une distribution de charge est égale à l'opposé de la variation d'énergie du champ électromagnétique moins le flux du vecteur de Poynting représentant ainsi la puissance sortante du champ.

Remarquons que si le volume considéré est vide de charges alors 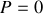et le flux du vecteur de Poynting représente la perte d'énergie du champ électromagnétique contenu dans ce volume.