De la même façon, si nous reprenons les ondes sphériques que nous avions considérées arbitrairement de la forme
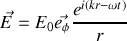
et
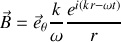
il vient pour la moyenne du vecteur de Poynting
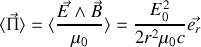
Remarquons encore une fois que ce vecteur est colinéaire au sens de propagation de l'onde ; si nous calculons le flux F du vecteur sur une sphère de rayon R centrée à l'origine il vient
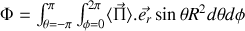
après intégration triviale
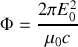
Ce flux total est donc constant par simplification des R2 ; a contrario, ce résultat intuitif de conservation de l'énergie nous explique pourquoi pour une onde à symétrie sphérique l'intensité locale sur un élément de surface décroît en carré de la distance, ce dont nous avons l'expérience quotidienne en nous éloignant d'une source ponctuelle.



