avec désormais supposé être une variable réelle proche de la valeur (espérance).

On cherche le maximum de ou de façon équivalente (le logarithme étant monotone) de .

puisque et la formule de Stirling (pour le logarithme de la factorielle) donne approximativement alors :

Si alors .

donc correspond au maximum de .

En développant au deuxième ordre autour de la valeur :

si :

donc : ce qui constitue l'approximation dite « normale » (courbe de Gauss).

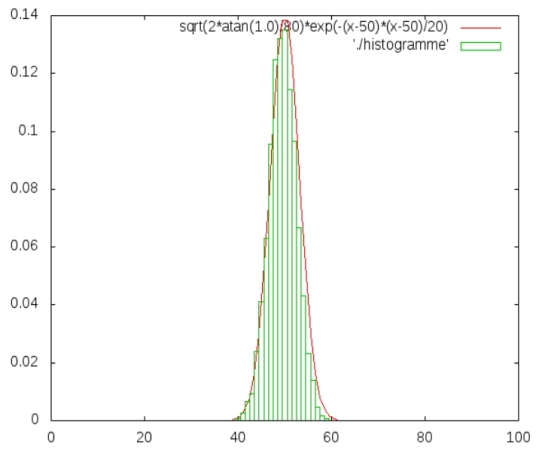
Comparaison de l'histogramme calculé avec des « tiroirs » de taille 1, et obtenu pour la somme de 100 nombres aléatoires entre 0 et 1 (expérience répétée sur ordinateur 10000 fois) et l'approximation normale, qui avec une variance de 10 coïncide avec le résultat de l'expérience. En effet, l'addition étant commutative, le résultat de cette expérience de moyenne évidemment égale à 50 est bien décrit par la distribution binômiale (l'ordre des facteurs n'importe pas).