Reprenons et supposons désormais (événement de faible probabilité, et expérience répétée un grand nombre de fois : par exemple, nombre de coups de pied de cheval reçus par des soldats dans l'armée prussienne, premier exemple historique d'application de cette loi, ou exemple de la désintégration radioactive).

Alors :

Si et : ,

or on a montré que l'espérance alors : ,

par conséquent ,

or et donc (1)

d'autre part nous avons supposé que alors

or alors (2).

Les deux équations (1) et (2) conduisent à :

nommée distribution de Poisson ,

or

: la condition de normalisation est satisfaite

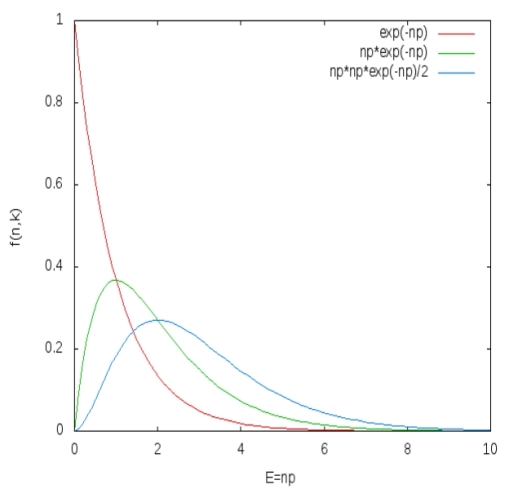
La distribution de Poisson nous donne donc la probabilité que événements se produisent par exemple pendant un certain intervalle de temps où l'espérance d'un événement est . On comprend bien que la probabilité que 0 événements se produisent décroisse rapidement avec le temps, que la probabilité que 1 événement se produise est faible pour les temps courts, augmente pour les temps proches de l'intervalle considéré, et diminue pour les temps plus longs alors que la probabilité d'en avoir plus de 1 augmente à son tour, etc.

Représentation graphique de f(k,n) en fonction de k