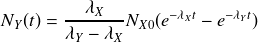On veut résoudre :
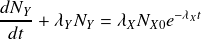
Forme de la solution :
Intuitivement, on voit que la résolution de l'équation sans second membre
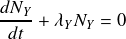implique que
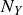soit de la forme :
.
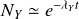De plus la forme du second membre implique que, pour que l'équation complète soit vérifiée, on doit avoir
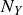du même type, c'est-à-dire :
.
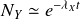On en déduit que l'on doit chercher une solution générale de la forme :
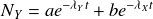, avec a et b constantes réelles.
Conditions initiales :
A
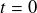, on suppose :
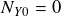
Donc
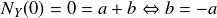
Donc
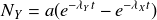
Détermination de la constante :
On remplace
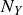dans l'équation différentielle complète :
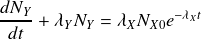
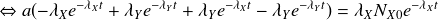
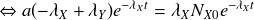
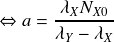
On obtient ainsi la solution générale :
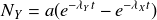, soit :
