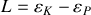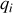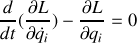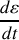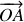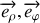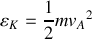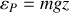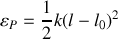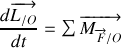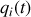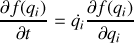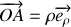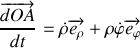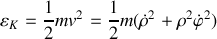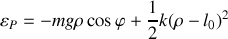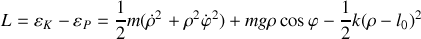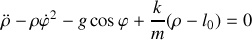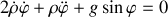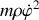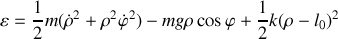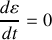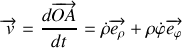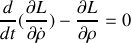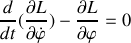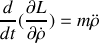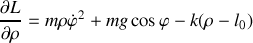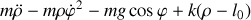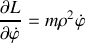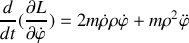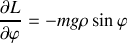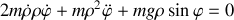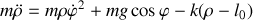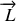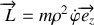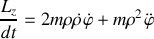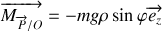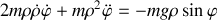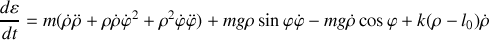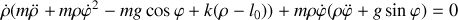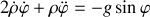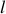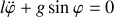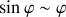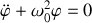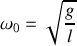Mécanique III - Théories de Lagrange et d'Hamilton

Pendule élastique

Énoncé

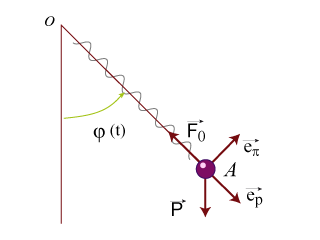
Un pendule élastique est constitué d'une tige mince de poids négligeable sur laquelle s'enroule un ressort de constante de raideur 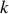de longueur à vide 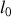. A l'extrémité du ressort est accrochée une masselotte 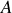considérée comme 'ponctuelle' de masse 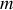. Le mouvement du système reste contenu dans un plan.

Figure

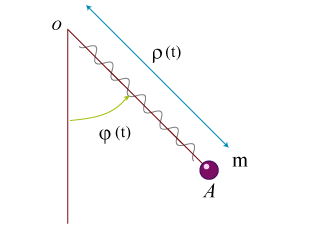
Quel est le nombre de degrés de liberté nécessaires pour décrire le mouvement de ?
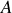Donner les coordonnées du point 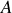. En déduire sa vitesse.
Ecrire l'énergie cinétique et l'énergie potentielle.
Donner le lagrangien et les équations du mouvement.
En analysant le mouvement selon la direction de la tige, identifier les forces qui contribuent au mouvement.
De quel théorème de mécanique vectorielle la seconde équation peut-elle être déduite ?
Donner l'énergie mécanique totale. Est-elle conservée ? Pourquoi ?
Montrer, en utilisant l'énergie mécanique totale, la question (7) et la seconde équation de Lagrange que l'on peut retrouver l'équation du mouvement selon la direction de la tige.
Si on remplace le ressort par une tige, comment se simplifient les équations ?

Aide simple

Aide détaillée

Solution détaillée

Figure

La tige supportant le ressort va osciller dans un plan. L'angle que fait l'axe de la tige avec la verticale est un degré de liberté.
De plus, l'élasticité du ressort introduit un deuxième degré de liberté, la distance du point à l'origine du repère. Au final, le système peut être décrit par 2 degrés de liberté.
Définissons le vecteur :
D'où la vitesse,
L'énergie cinétique s'écrit :
La force élastique et le poids dérivent d'une énergie potentielle.
avec la position (plan ) comme origine de l'énergie potentielle de pesanteur.
On en déduit le lagrangien :
Ecrivons les 2 équations de Lagrange :
et
et
d'où l'équation différentielle suivante :
L'équation suivant la direction de la tige s'écrit en multipliant par :

On retrouve le principe fondamental de la dynamique avec la contribution du poids suivant cette direction, la force de rappel du ressort ainsi que la force d'inertie centrifuge ( ) liée à l'entraînement du pendule suivant .
La seconde équation représente le théorème du moment cinétique .

Seul le poids contribue à la somme des moments.

On retrouve la 2ième équation.
L'énergie mécanique totale s'écrit:
Les forces extérieures, pesanteur et force élastique, dérivent d'une énergie potentielle. L'énergie mécanique est donc conservée.
or d'après (7) :

On retrouve alors l'équation de Lagrange selon la direction de la tige.
Si on remplace le ressort par une tige, n'est plus un degré de liberté car la tige a une longueur fixe . Il ne reste plus que comme degré de liberté.

Dans l'approximation des petits angles,
On retrouve l'équation différentielle du pendule simple de pulsation

Début