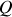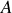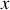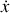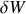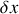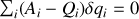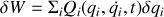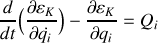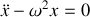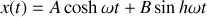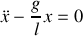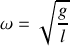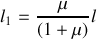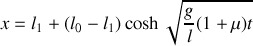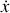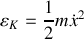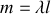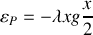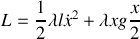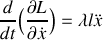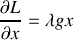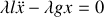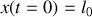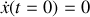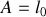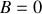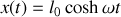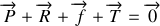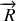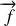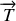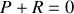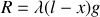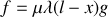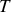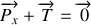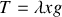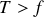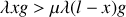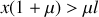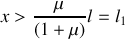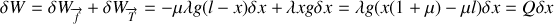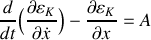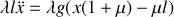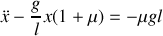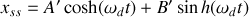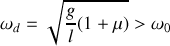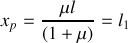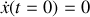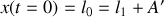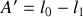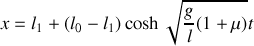Soit
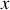 la distance de l'extrémité pendante au bord de la table à tout instant.
la distance de l'extrémité pendante au bord de la table à tout instant.
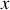 sera la coordonnée généralisée.
sera la coordonnée généralisée.
Toute la chaîne se déplace à la même vitesse
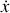 , d'où l'énergie cinétique de la chaîne:
, d'où l'énergie cinétique de la chaîne:
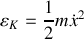 avec
avec
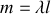 .
.
Seule la partie de chaîne suspendue est soumiseà l'accélération de la pesanteur. Pour la partie horizontale, le poids et la réaction de la table se compensent.
Ce qui donne pour l'énergie potentielle:
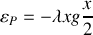 en prenant le milieu de la partie suspendue.
en prenant le milieu de la partie suspendue.
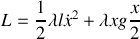
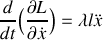
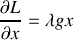
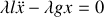
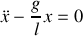
La solution d'une telle équation s'écrit :
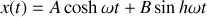 avec
avec
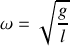 .
.
Avec les conditions initiales
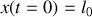 et
et
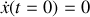 , on a
, on a
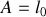 et
et
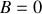 , d'où la solution :
, d'où la solution :
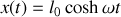 .
.
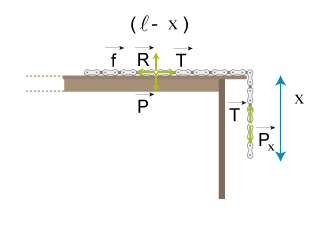
Ecrivons le principe fondamental de la dynamique pour la partie horizontale à l'équilibre.
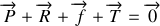 avec
avec
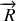 la réaction normale du support,
la réaction normale du support,
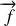 la force de frottements solide horizontale et
la force de frottements solide horizontale et
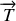 la tension du fil.
la tension du fil.
Projetons sur la verticale:
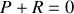 , soit
, soit
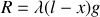 .
.
Selon l'horizontale,
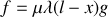 .
.
Pour trouver
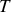 , écrivons l'équilibre pour la partie suspendue :
, écrivons l'équilibre pour la partie suspendue :
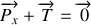 , soit
, soit
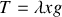 .
.
Pour qu'il y ait mouvement, il faut que
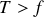 soit
soit
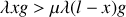 , soit
, soit
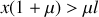 .
.
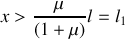
La tension et les frottements sont les forces qui travaillent pour la partie en frottements sur la table.
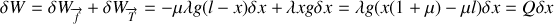 ,
,
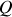 étant la force généralisée.
étant la force généralisée.
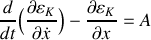 ,
,
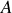 étant l'accélération généralisée avec
étant l'accélération généralisée avec
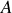 =
=
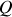 .
.
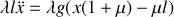
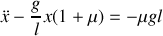
On obtient une équation différentielle avec second membre. La solution générale sans second membre s'écrit :
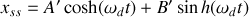 , avec
, avec
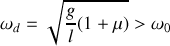 .
.
Une solution particulière est :
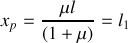 .
.
Avec les conditions initiales
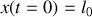 et
et
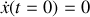 ,
,
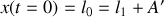 d'où
d'où
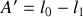 .
.
On en déduit la solution générale:
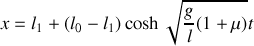 .
.
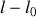 d'une chaîne de longueur
d'une chaîne de longueur
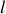 , de masse linéique
, de masse linéique
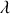 constante, repose à l'instant initial rectilignement sur une table horizontale. L'autre partie, de longueur
constante, repose à l'instant initial rectilignement sur une table horizontale. L'autre partie, de longueur
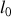 , pend selon la verticale. On lâche la chaîne sans vitesse initiale.
, pend selon la verticale. On lâche la chaîne sans vitesse initiale. 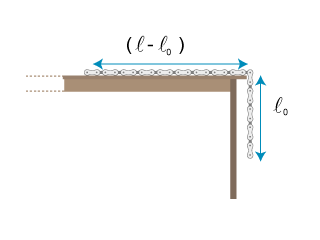
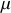 constant. Quelle est la longueur
constant. Quelle est la longueur
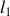 minimale nécessaire pour que la corde se mette en mouvement ? Si
minimale nécessaire pour que la corde se mette en mouvement ? Si
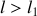 , écrire et résoudre l'équation de Lagrange.
, écrire et résoudre l'équation de Lagrange.