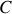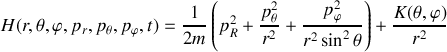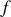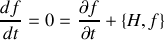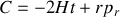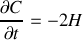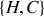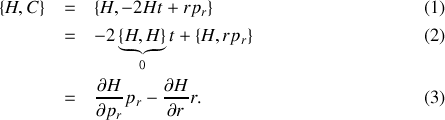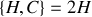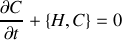Énoncé
On considère une particule de masse
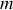se déplaçant dans l'espace à trois dimension et soumise à un potentiel
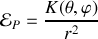
avec
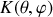l une fonction quelconque des angles de la base sphérique et et
la distance à l'origine.
Trouver le Hamiltonien
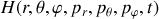de la particule en coordonnées sphériques.Montrer que la quantité
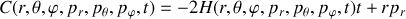est conservée.
