Énoncé
Deux masses ponctuelles
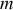 identiques sont placées aux extrémités d'une tige rigide de longueur
identiques sont placées aux extrémités d'une tige rigide de longueur
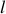 et de masse négligeable. Initialement, la tige est maintenue verticale, une extrémité touchant le sol. La tige est maintenant lâchée sans vitesse initiale et l'on suppose que l'extrémité glisse parfaitement sur le sol.
et de masse négligeable. Initialement, la tige est maintenue verticale, une extrémité touchant le sol. La tige est maintenant lâchée sans vitesse initiale et l'on suppose que l'extrémité glisse parfaitement sur le sol.
Donner le nombre de degrés de liberté du système.
Déterminer le Lagrangien
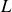 du système; en déduire le Hamiltonien.
du système; en déduire le Hamiltonien.En déduire quatre intégrales premières du mouvement et les interpréter physiquement.
Exprimer la vitesse de l'extrémité supérieure lorsqu'elle touche le sol.
Pour déterminer le nombre de degrés de liberté, déterminer d'abord les contraintes géométriques.
Calculer l'énergie cinétique et l'énergie potentielle, paramétrer la position de la barre en utilisant la position du centre de gravité des deux masses et deux angles définissant l'orientation spatiale de la barre.
Pour paramétrer le système, placer un repère cartésien dont les axes
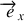 et
et
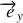 sont contenus dans le plan horizontal et la barre étant initialement confondue avec l'axe
sont contenus dans le plan horizontal et la barre étant initialement confondue avec l'axe
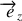 . En appelant
. En appelant
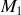 le point matériel assujetti à se déplacer dans le plan
le point matériel assujetti à se déplacer dans le plan
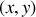 , donner les coordonnées de
, donner les coordonnées de
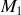 dans une base polaire du plan
dans une base polaire du plan
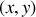 . Déterminer les coordonnées de l'autre point matériel
. Déterminer les coordonnées de l'autre point matériel
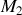 en utilisant une base cylindrique.
en utilisant une base cylindrique.
NLP_C_M03_G03
Il y a 4 degrés de liberté
La paramétrisation du système est décrite sur la figure 1.
Le Lagrangien vaut
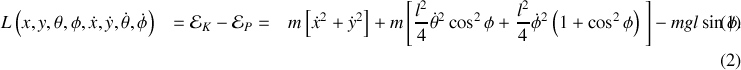
Le hamiltonien vaut
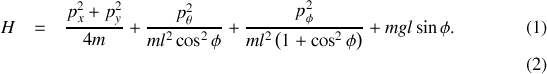
Les intégrales premières du mouvement sont
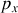 et
et
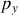 les impulsions horizontales du centre de gravité,
les impulsions horizontales du centre de gravité,
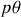 qui est à un facteur près la projection du moment cinétique sur l'axe vertical
qui est à un facteur près la projection du moment cinétique sur l'axe vertical
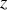 et
et
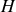 l'énergie mécanique
l'énergie mécanique Au contact la vitesse de l'extrémité supérieur est verticale descendante et de module
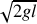 .
.
Le système est composé de 2 points matériels évoluant dans l'espace et possédant 2 contraintes géométriques: la masse inférieure est assujettie à se déplacer dans le plan et la masse supérieur doit rester à distance fixe de la masse inférieure. Les 2 points matérielles ont chacun
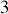 degrés de liberté soit
degrés de liberté soit
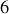 au total, en soustrayant les deux contraintes, on obtient
au total, en soustrayant les deux contraintes, on obtient
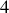 degrés de liberté.
degrés de liberté.La paramétrisation du système est décrite sur la figure 1. Les variables
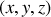 sont les coordonnées cartésiennes du centre de gravité
sont les coordonnées cartésiennes du centre de gravité
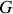 . Les angles
. Les angles
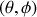 caractérisent l'orientation de la barre dans l'espace:
caractérisent l'orientation de la barre dans l'espace:
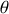 est l'angle entre la projection de la barre dans le plan
est l'angle entre la projection de la barre dans le plan
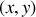 et l'axe
et l'axe
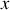 ,
,
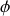 est l'angle entre la barre et le plan
est l'angle entre la barre et le plan
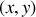 .
.Une extrémité de la barre étant constamment dans le plan
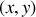 , la variable
, la variable
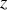 ne dépend de
ne dépend de
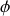 et l'on a
et l'on a
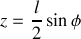 .
.Les deux masses étant égales,
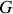 est au milieu de la barre. Les quatre coordonnées généralisées sont donc
est au milieu de la barre. Les quatre coordonnées généralisées sont donc
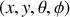 .
. On obtient aisément l'énergie potentiel
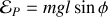 .
.Pour le calcul de l'énergie cinétique, il faut procéder au calcul préalable des vitesses
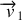 et
et
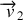 des masses
des masses
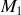 et
et
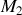
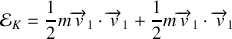
On commence donc par déterminer les vecteurs positions en passant par le centre de gravité:
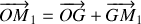
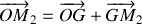
en notant que
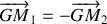 On peut maintenant déterminer les vecteurs vitesses:
On peut maintenant déterminer les vecteurs vitesses: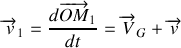
et
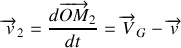
avec
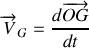 et
et
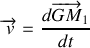 que l'on calculera ultérieurement.
que l'on calculera ultérieurement.Dès lors, il vient pour l'énergie cinétique
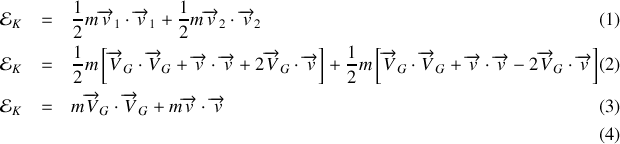
L'énergie cinétique est composée de deux termes, le premier caractérise l'énergie cinétique du centre de masse et l'autre l'énergie cinétique de rotation de la barre.
En calculant maintenant les vecteurs vitesses:
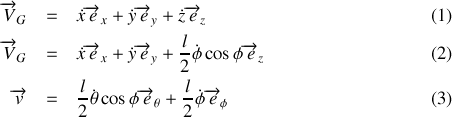
on obtient
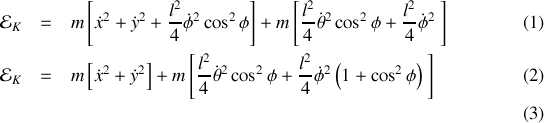
Soit pour le Lagrangien
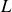
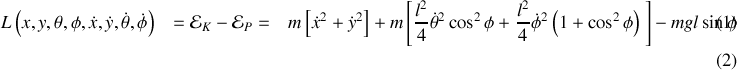
On détermine ensuite les impulsions généralisées
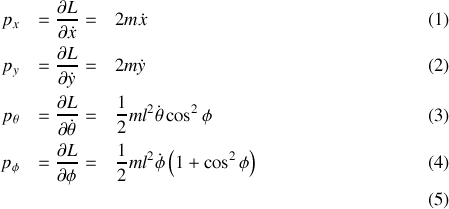
puis l'Hamiltonien
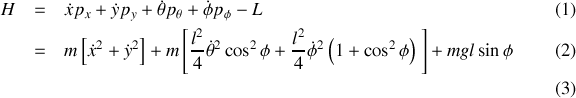
Il reste enfin à introduire les impulsions généralisées dans le hamiltonien.
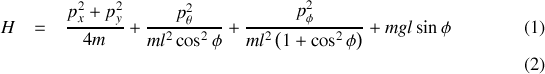
Les variables
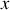 ,
,
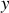 , et
, et
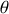 sont cycliques, les trois impulsions correspondantes sont donc des constantes du mouvement.
sont cycliques, les trois impulsions correspondantes sont donc des constantes du mouvement.Les impulsions
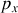 et
et
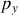 correspondent aux projections de l'impulsion du centre de masse dans le plan horizontal, il est logique de les retrouver comme constante du mouvement puisque les seules forces extérieures agissant sur le système (les poids et la réaction normale du support) alignées suivant la verticale ne peuvent faire varier l'impulsion horizontale.
correspondent aux projections de l'impulsion du centre de masse dans le plan horizontal, il est logique de les retrouver comme constante du mouvement puisque les seules forces extérieures agissant sur le système (les poids et la réaction normale du support) alignées suivant la verticale ne peuvent faire varier l'impulsion horizontale. L'impulsion
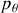 est liée à la projection du moment cinétique dans la direction verticale. Encore une fois, les forces extérieures étant alignées suivant la verticale, leurs moments suivant l'axe
est liée à la projection du moment cinétique dans la direction verticale. Encore une fois, les forces extérieures étant alignées suivant la verticale, leurs moments suivant l'axe
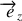 sont nuls et il ne peut donc y avoir de variation du moment cinétique dans cette direction.
sont nuls et il ne peut donc y avoir de variation du moment cinétique dans cette direction. Enfin, si l'on ajoute l'hamiltonien qui représente l'énergie mécanique, on obtient les quatre intégrales premières du mouvement.
Si à l'instant initial, la barre est verticale et qu'elle est lâchée sans vitesse alors
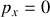 ,
,
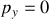 et p_
et p_
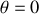 et l'énergie mécanique vaut
et l'énergie mécanique vaut
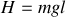 .
. Lorsque la barre arrive dans le plan horizontal (
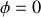 ) la vitesse de l'extrémité est telle que
) la vitesse de l'extrémité est telle que 
soit encore
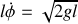
La vitesse de l'extrémité supérieur vaut donc
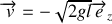 .
.



