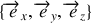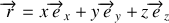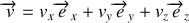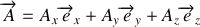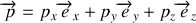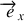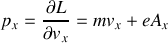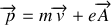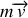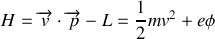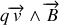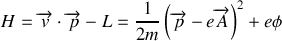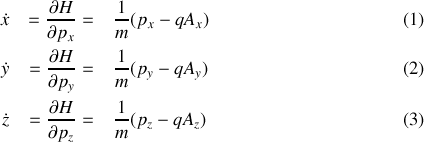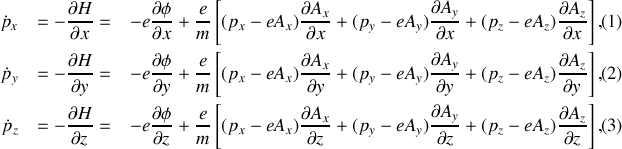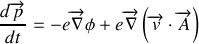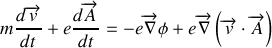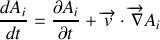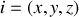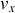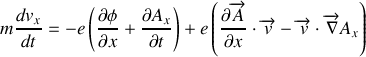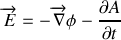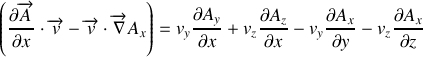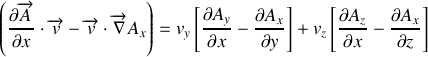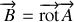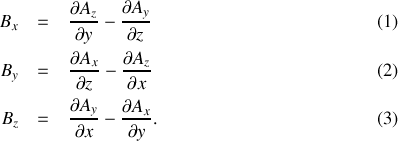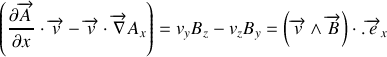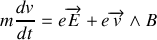L'impulsion est obtenue à partir du Lagrangien en le dérivant par rapport à la vitesse. Pour cela, on introduit une base cartésienne
 dans laquelle on décompose le vecteur position
dans laquelle on décompose le vecteur position
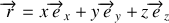 , le vecteur vitesse
, le vecteur vitesse
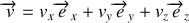 , le potentiel vecteur
, le potentiel vecteur
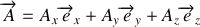 et le vecteur impulsion
et le vecteur impulsion
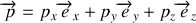 .
.
On obtient les composantes de l'impulsion en dérivant le Lagrangien par rapport à chaque composante de la vitesse.
Ainsi pour la composante sur
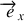 , on obtient :
, on obtient :
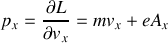 ,
,
les autres composantes s'obtiennent de manière analogue, si bien que finalement
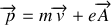 .
.
On voit dans cette exemple que l'impulsion n'est pas égale à la quantité de mouvement
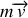 , c'est une conséquence de la dépendance du potentiel en la vitesse.
, c'est une conséquence de la dépendance du potentiel en la vitesse.
Le Hamiltonien se déduit du Lagrangien :
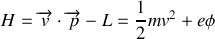 .
.
On remarque que le Hamiltonien, qui représente l'énergie, ne dépend pas du potentiel vecteur. Cela implique que le champs magnétique n'intervient pas dans l'énergie du système. Or, il est bien connu que la force magnétique
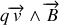 , étant perpendiculaire à la vitesse ne travaille pas et donc ne fait pas varier l'énergie. On retrouve ici ce résultat classique.
, étant perpendiculaire à la vitesse ne travaille pas et donc ne fait pas varier l'énergie. On retrouve ici ce résultat classique.
En utilisant l'expression de l'impulsion, l'Hamiltonien s'écrit aussi :
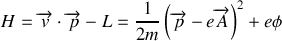 .
.
Les premières équations de Hamilton nous redonnent la relation entre impulsion et vitesse
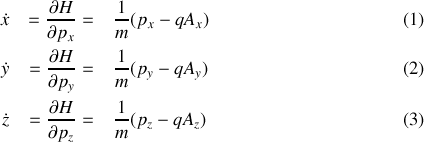
Quant aux secondes :
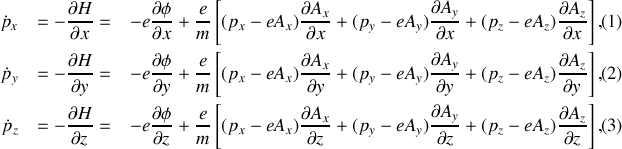
elles peuvent s'écrire sous la forme :
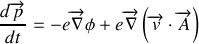
Pour retrouver les équations de Newton, il faut remplacer $\overrightarrow{p}$ des secondes équations par sont expression issue des premières ainsi :
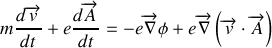 .
.
soit en remarquant
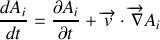 où
où
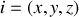 on obtient les équations projetées. On donne ici l'équation déterminant la composant
on obtient les équations projetées. On donne ici l'équation déterminant la composant
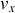
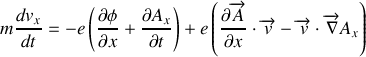
On reconnaît dans le premier terme du membre de droite la composante suivant
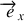 du champ électrique : (
du champ électrique : (
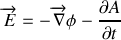 ).
).
Le second terme a pour expression :
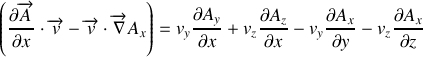
que l'on peut mettre sous forme :
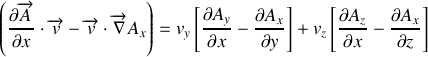
Le champs magnétique, définit par la relation :
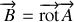 , a pour composante
, a pour composante
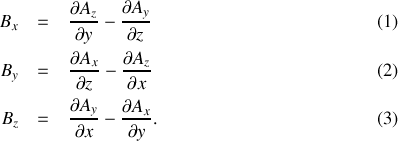
Ainsi :
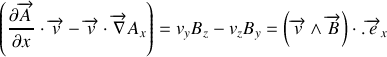 .
.
Les calculs des autres composantes se déduit par permutation circulaire des indices et l'on retrouve effectivement la loi de Newton avec la force de Lorentz :
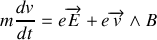 .
.
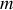 et de charge
et de charge
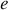 est plongée dans un champ électromagnétique que l'on décrit par le potentiel scalaire
est plongée dans un champ électromagnétique que l'on décrit par le potentiel scalaire
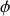 et par le potentiel
et par le potentiel
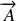 . On suppose ici que
. On suppose ici que
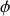 et
et
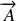 ne dépendent pas du temps.
ne dépendent pas du temps.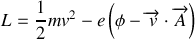 .
.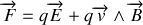 .
.