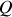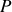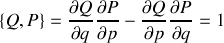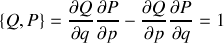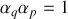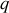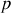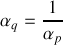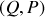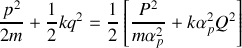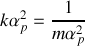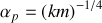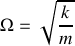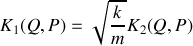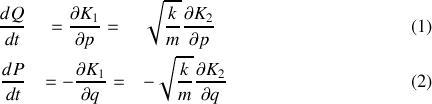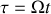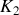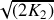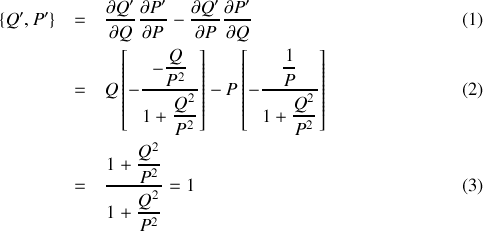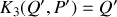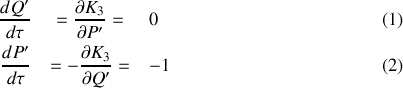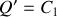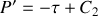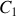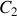Énoncé
Déterminer, en utilisant les crochets de Poisson, une condition sur les paramètres
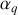et
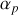pour que le changement de variable
soit canonique (voir rappel de cours).
Montrer qu'un oscillateur harmonique de masse
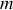et de raideur
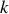décrit par le hamiltonien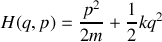 
peut aussi être décrit par un Hamiltonien
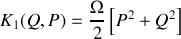
en utilisant la transformation canonique de la question précédente. Préciser la valeur des paramètres
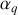et
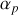.Montrer qu'en renormalisant le temps ce même système peut être caractérisé par un nouveau hamiltonien
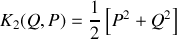. Indiquer alors la relation entre le temps vrai
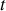et le temps renormalisé
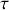. Donner la nature des trajectoires dans l'espace des phases. On souhaite faire un nouveau changement de variable afin d'exploiter au mieux la conservation de l'énergie, on pose alors
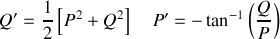,montrer que ce changement de variable est canonique. Déterminer les équations de Hamilton à l'aide des variables
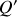et
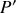et les résoudre. Interpréter géométriquement ces nouvelles variables dans l'espace des phases
.
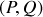