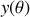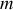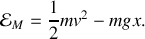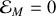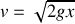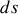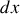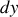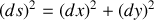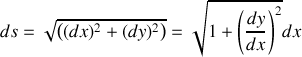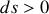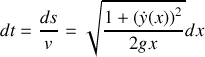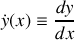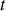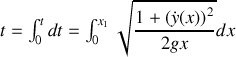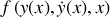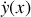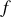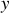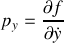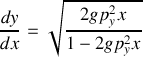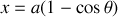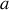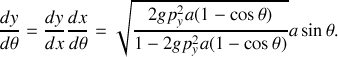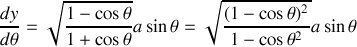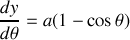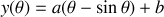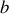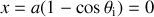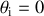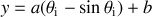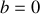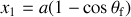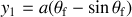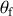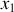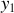Énoncé
On désire trouver une courbe
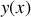entre deux points fixes du plan
telle qu'une particule glissant sans frottements le long de la courbe en partant avec une vitesse initiale nulle, fasse le trajet en un temps minimum. On supposera que le mouvement est du à un champ de gravitation constant. On appelle
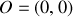le point de départ et
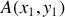le point d'arrivé
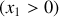; l'axe
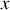est aligné sur la verticale descendante.
Montrer que le temps de parcours s'exprime comme une intégrale sur x dépendant de
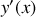.Faire l'analogie avec l'action mécanique et en déduire une équation différentielle pour la courbe
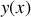dont la solution minimise le temps de parcours.Identifier une intégrale première de cette équation différentielle.
Déterminer l'équation de la courbe recherchée.
